1. Алгебра
  2. 2sin²x-7sinx+3=0 Найти корни,

2sin²x-7sinx+3=0 Найти корни, удовлетворяющие с с объяснением

Андрей14411 Андрей14411    1   30.08.2020 00:38    1

Ответы
Alex30050 Alex30050  15.10.2020 16:25

2sin^2x-7sinx+3=0

Делаем замену:

sinx=t

Не забываем про условие

- 1 \leqslant t \leqslant 1

Получаем квадратное уравнение :

2t^2-7t+3=0

Решаем:

D=49-4*3*2=25\\t_1=3\\t_2=\frac {1}{2}

Первый корень не удовлетворяет условию

- 1 \leqslant t \leqslant 1

А вот второй корень нам подходит.

Делаем обратную замену:

sinx=\frac{1}{2}

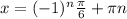
x=(-1)^n\frac{\pi} {6}+\pi n

ответ:

x=(-1)^n\frac{\pi} {6}+\pi n

б) Смотрим на рисунок.

Наши решения располагаются в первой и во второй четвертях.

А решения условия

cosx \leqslant 0

располагаются во второй и в третьей

четвертях.

Поэтому решение уравнения

x=\frac{\pi} {6}+2\pi n

не удовлетворяет поставленному условию.

Но зато решение

x=\frac{5\pi} {6}+2\pi n

нам вполне подходит.

ответ:

x=\frac{5\pi} {6}+2\pi n


2sin²x-7sinx+3=0 Найти корни, удовлетворяющие с с объяснением
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Franker10 Franker10  27.02.2021 12:34
Постройте в одной и той же координатной плоскости графики функций у=х² и у=-x+6 и найдите координаты точек пересечения этих графиков​...
vladyslav2523 vladyslav2523  27.02.2021 12:34
Контрольная работа по трёхчленам !...
Sunlight11 Sunlight11  27.02.2021 12:34
Найдите наибольший корень уравнения2х^2 + (6 - √3)x = 3√3.А) 3В) √3C) 2√3D) 0,5 √3​...
янасеребрянская3012 янасеребрянская3012  27.02.2021 12:35
Какие из следующих чисел заключено между числами 4 дробь 11 и 7 дробь 17? 1)0,1; 2)0,2; 3)0,3; 4)0,4:​...
Белова1234567890 Белова1234567890  27.02.2021 12:36
Задание по алгебре во вложении картинка)...
Расулев Расулев  07.10.2019 20:10
Выражение 2y-7y, b^2+b^2+b^2, -6x-10x, -2+9x-9x, 7b^2-3b^2+2b^2...
SSEMAA SSEMAA  07.10.2019 20:10
Саяхатшылар бірінші күні барлық жолдың 38%-ін, екінші күні 26%-ін жүрді. қалған 9 км-ді үшінші күні жүрді. саяхатшылар барлығы қанша км жол жүру керек еді?...
marylist2005 marylist2005  07.10.2019 20:10
Решить уравнение: 2)(3+4х)(16х^2-12х+9)-64х^3=-10х. заранее.​...
Maximp190302 Maximp190302  07.10.2019 20:10
Решите неравенства (3х-1)^2-7 (9х+2)х+2 2х(8х+3)+1 (5-4х)^2-1...
Адема12345 Адема12345  07.10.2019 20:10
Два экскаватора, работая одновременно, могут вырыть котлован за 4ч 48 мин. если же сначала первый экскаватор выроет самостоятельно ¼ котлована, а затем второй – оставшуюся часть...

Популярные вопросы