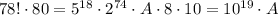13. n, ae n
78! + 79! = a * 10^n
max(n) = ?
a) 15 b) 16 c) 17 d) 18
e) 19
Другие вопросы по теме Алгебра
Популярные вопросы
- Из пункта а в пункт б(расстояние от пункта а до пункта б 7,5км)...
2 - Напишите уравнения реакции горения магния,угля,железа,метана....
1 - Определи склонение существительных по начальной форме и выпеши...
3 - Поле площадью 2,4 га разделили на два участка,найдите площадь...
3 - Ккакой части речи относятся слова-всем и тогда...
3 - Почему отвергнув любовь татьяны онегин сам влюбляется в нее?...
3 - За 8 минут самолет, двигаясь с одинаковой скоростью, пролетел...
1 - Если путешествиник будет идти от деревни а до города в со скоростью4.5...
2 - Тракторист в первый день вспахал 4/13 всего поля, во второй 3/11...
2 - Найважливіші події що відбулися на українських землях 60-800-х...
2
По свойству степеней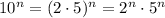 и 2,5, - простые.
и 2,5, - простые.
Подсчитаем сколько раз входит число 2 в факториал 78
То есть, в числе 78! двойка встречается 74 раза.
Подсчитаем сколько раз входит число 5 в факториал 78
В числе 78! пятерка встречается 18 раз.
Таким образом,