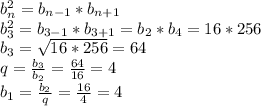1: система x-y=4 xy = 5 2 : найдите любые два решения данного неравенства у< или равно 3х в квадрате+1 3: найдите десятый член и сумму двадцати первых членов арифметической прогрессии: 2; 9; 16; 23 4: дано: cos альфа=три пятых, вычислить sin альфа, tg альфа, ctg альфа. 0< альфа< пи делить на 2 5: если второй член геом. прогрессии равен 16, а четвертый член равен 256, найдите первый член и знаменатель прогрессии !
Другие вопросы по теме Алгебра
Популярные вопросы
- Решите войско, состоящее из шести компьютерных героев, необходимо вооружить...
2 - Выбери два имени существительного из текстов и проведи морфологический...
2 - Пямоугольникаfdnm,если-площадь-треугольникаflm-равна225мм(2) dl-1см ln-2,7см...
1 - Подчеркни прилагательные , надпиши сверху род и число. маленькое дело...
1 - Из перечня организаций выберите те, которые представляют гражданское...
2 - Выпишите существительные, обозначьте в них суффиксы. люблю березу , то...
3 - Из перечня выберите правоотношения, не являющиеся административными:...
2 - Сторона основания правильной прямоугольной призмы abca1b1c1 равна 2,...
2 - 1/4 х (-3)+1/7 пож решить нужно для мониторинга...
3 - Напишите год рождения пушкина 1799 и дату войны 1941-1945 римскими цифрами...
1
1)
y1=1 y2=-5
x1=4+1=5 x2=4-5=-1
2)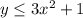
y=1 y=-3
x=0 x=-3
3)d=9-2=7
a1=2
4)Т.к. угол 1 четверти, тогда значения sin , cos положительные.
5)