1) Постройте график функции f(x)=2x^2-(a+2)x+a, если известно, что её нули x1 и x2 связаны соотношением 1/х1 + 1/х2 =3
2) Постройте график функции f(x)= x^2 +3x +a, если известно, что её нули х1 и х2, связаны соотношением х1^2•х2+х1•х
Другие вопросы по теме Алгебра
Популярные вопросы
- Какие образы произведения алые паруса вы считаете символическими? и еще...
1 - Complete the disjunctive questions. 1. пример 2. aren t i? 3. isn,t there?...
2 - Втуристическом автобусе 39 посадочных мест. на экскурсию желают поехать...
3 - Иней это множестве число или единствн...
3 - Дать определения слову месть, определение и аргумент из собственного...
1 - Обьясните понятие. греческий огонь...
1 - Два поезда одновременно отправились от одной станции в противоположных...
2 - Решить примеры в столбик с остатком 4380: 600= 13590: 300=...
1 - Назовите ключевые слова, необходимые для характеристики центральных образов...
3 - Сочинение на тему письмо на анг на завтра нада...
2
Нули функции:
Согласно теореме Виета, имеем:
По условию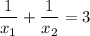 или
или 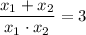 .
.
Следовательно, подставляя значения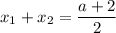 и
и 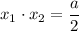 , найдем параметр
, найдем параметр  :
:
Таким образом,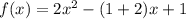 , то есть
, то есть 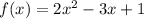
Найдем координаты точки вершины параболы:
Значит,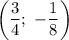 — точка вершины параболы.
— точка вершины параболы.
Найдем точки пересечения с осями координат:
а) С осью абсцисс:
Следовательно,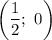 и
и 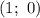 — точки пересечения функции с осью абсцисс.
— точки пересечения функции с осью абсцисс.
б) С осью ординат:
Следовательно,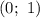 — точка пересечения с осью ординат.
— точка пересечения с осью ординат.
Согласно свойству симметрии параболы,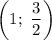 — точка графика.
— точка графика.
Изобразим график данной функции (см. вложение).
Нули функции:
Согласно теореме Виета, имеем:
По условию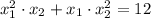
Следовательно, подставляя значения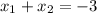 и
и 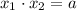 , найдем параметр
, найдем параметр  :
:
Таким образом,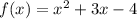
Найдем координаты точки вершины параболы:
Найдем точки пересечения с осями координат:
а) С осью абсцисс:
Следовательно,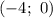 и
и 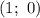 — точки пересечения функции с осью абсцисс.
— точки пересечения функции с осью абсцисс.
б) С осью ординат:
Следовательно, — точка пересечения с осью ординат.
— точка пересечения с осью ординат.
Согласно свойству симметрии параболы, — точка графика.
— точка графика.
Изобразим график данной функции (см. вложение).