1. дано f'(x)=x^3 найти f'(-1) 2. решите уравнение 4^x-2=(1/4)^2x-1 3. вычислите интеграл от 1 до 2 x^4dx 4. найдите минимумы функции f(x)=3x-x^3

1)f`(-1)=(-1)^3=-1

2)4^x-2=4^1-2x, x-2=1-2x, 3x=3,x=1

3)X^5/5 от 1 до 2, 2^5/5- 1^5/5=31/5

4)найдем производную f`(x)=3-3x^2.приравняем к нулю.

3x^2=3, x^2=1, x=+-1. они же и являются точками минимума

1)

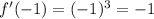
2) 

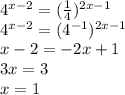
3)

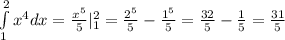
4)

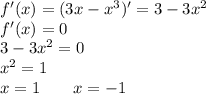
x=1 - точка максимума функции.

х=-1 - точка минимума функции.