1. Алгебра
  2. 1.дана прогрессия 2; 4; 8; а)найдите

1.дана прогрессия 2; 4; 8; а)найдите 6 член прогрессии б) сумму первой 6-ти членов членов прогрессий 2.найдите сумму бесконечной прогрессии (bn),если b1=24 q=1/2 3. в прогрессий (сn) c4=24 ; q=-2 а)найдите с1 б)какие из чисел данной прогресии отрицательны? 4.дана бесконечная прогрессия (сn) с суммой s=15 и первым членом с1=18. найдите q.

lisafoxxxxxxxx lisafoxxxxxxxx    2   24.04.2019 07:20    0

Ответы
СтарыйМатематик СтарыйМатематик  08.06.2020 14:46

1. Разность геометрической прогрессии: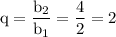 \rm q=\dfrac{b_2}{b_1}=\dfrac{4}{2}=2

Используем n-ый член геометрической прогрессии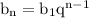 \rm b_n=b_1q^{n-1}

a)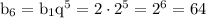 \rm b_6=b_1q^5=2\cdot 2^5=2^6=64

Сумма первых шести членов геометрической прогрессии вычисляется по следующей формуле: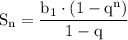 \rm S_n=\dfrac{b_1\cdot \left(1-q^n\right)}{1-q}

б)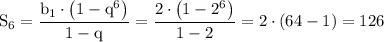 \rm S_6=\dfrac{b_1\cdot \left(1-q^6\right)}{1-q}=\dfrac{2\cdot\left(1-2^6\right)}{1-2}=2\cdot(64-1)=126


2. Сумма бесконечно убывающей геометрической прогрессии вычисляется по формуле: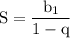 \rm S=\dfrac{b_1}{1-q}


\rm S=\dfrac{24}{1-\dfrac{1}{2}}=48


3. Используем n-ый член геометрической прогрессии, имеем

а)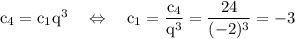 \rm c_4=c_1q^3~~~\Leftrightarrow~~~c_1=\dfrac{c_4}{q^3}=\dfrac{24}{(-2)^3}=-3

б) - непонятно что там


4. Используем сумму бесконечно убывающей геометрической прогрессии и отсюда найдем знаменатель прогрессии

\rm S=\dfrac{c_1}{1-q}~~~\Leftrightarrow~~~q=1-\dfrac{c_1}{S}=1-\dfrac{18}{15}=-0.2

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
вау39 вау39  27.01.2021 17:54
Логарифмическое неравенство.Награда ​...
kerimagaevakk kerimagaevakk  27.01.2021 17:53
Дана функция f(x)=−8^2+11. Заполните таблицу значений функции...
azodanic12 azodanic12  22.05.2019 17:10
16 в степени х-2*12 в степени х =3 в степени 2х+1...
Локи30 Локи30  22.05.2019 17:10
Одно число больше второго на 6, а их отношение 9: 7. найти эти числа...
Kroq123 Kroq123  22.05.2019 17:10
Решить ! зарание огромное 12x -7 при x=0.05 x+3.2 при x=-3.2...
kotyaraasm kotyaraasm  22.05.2019 17:10
Поделить число 472 на такие три части, чтобы 50% первой части были равны 60% второй и 80% третьей части...
MorficTV MorficTV  22.05.2019 17:10
При каком значении p прямая у= -х + р имеет м параболой у= х^2 + 3х ровно одну общую точку? найдите координаты этой точки. постройте в одной системе координат данную параболу...
maja6 maja6  22.05.2019 17:10
Найдите сумму первых пятнадцати членов арифмитической прогрессии, для которой а1=6 а10=33 (ответ: d=3, 405)...
simsnothave simsnothave  22.05.2019 17:10
Решить! разложите на множители: x^3 + y^6...
pelmenev777 pelmenev777  22.05.2019 17:10
При каких значениях параметра а график функции y=ax^2 - 2x + 2a + 1 имеет с осью абсцисс одну общую точку?...

Популярные вопросы