1) 3sin² x-4sin*cosx + cos² x=0 2) решите уравнение : sin²x - 9sinx*cosx+3 cos²x=-1 3) найдите корни уровнения : корень из 3 sin2x=cos2x принадлежащие отрезку [-1; 4]
Другие вопросы по теме Алгебра
Популярные вопросы
- На каждом из 5 листов бумаги написано по одной букве (не повторяющиеся): A,...
3 - Егер шеңбердің радиусы 4 см,ал центрінен түзуге дейінгі қашықтық: а)3;ә)4 см;б)5...
2 - Кислая среда будет наблюдаться при растворении в воде...
2 - Напиши эссе Язык современного человека,, объём на более 120 слов...
2 - Определи ряд, состоящий только из натуральных чисел. 12; 1458; 9999; 104; 4;...
2 - В каких местах побывали главные герои из Дети капитана Гранта ? Опишите климат...
2 - «Тарих» ұғымы қандай мағынаны білдіреді?Бүгіннен бастап меңгеретін «Қазақстан...
2 - Байлық, байтақ жер,бақытты ел,асқар шыңды таулар,...
3 - Отрезок, длиной 52 см, двумя внутренними точками разделен на три отрезка. Длина...
2 - Егер доғал бұрыш α үшін оның ctgα=- 2/3 екені белгілі болса, sinα,cosα және...
3
1) разделим на cos^2x
3tg^2x-4tgx+1=0
3t^2-4t+1=0
D=16-4*3=4
t12 = (4+-2)/6
t1 = 1
t2 = 1/3
tgx = 1 tgx = 1/3
x = П/4 + Пk x = arctg(1/3) + Пk
2) sin²x - 9sinx*cosx+3 cos²x=-cos²x - sin²x
2sin²x - 9sinx*cosx+ 4cos²x = 0 |:cos²x
2tg^2x - 9tgx + 4 = 0
2t^2 - 9t + 4 = 0
D=81-4*2*4 = 49
t12 = (9+-7)/4
t1 = 4, t2 = 1/2
tgx = 4 tgx = 1/2
x = arctg4 + Пk x = arctg(1/2) + Пk
3)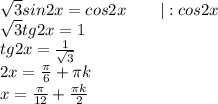
1. Делим на cos^2x
3sin^2x/ cos^2x - 4 sinx/cosx +1 = 0
3tg^2X - 4 tgx +1=0
пусть tgx = t
3t^2-4t+1=D= 16-12=4
t1=4+2/6 = 1
t2 = 4-2/6=1/3
1)tgx=1 2)tgx = 1/3
x = П/4+Пn, nєZ x= arctgx1/3+Пn, nєZ
2. sin²x - 9sinx*cosx+3 cos²x=-sin^2x - cos^2x
sin²x - 9sinx*cosx+3 cos²x+sin^2x + cos^2x=0
2sin²x- 9sinx*cosx+4 cos²x=0 /cos^2x
2th^2x - 9tgx +4=0
tgx=t
2t^2-9t+4=0
D=31-32 =49
t1=4
t2=1/2
1) 2)
tgx=4 tgx=1/2
x=arctg4 +Пn, nєZ x=arctg1/2+Пn, nєZ