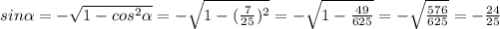Знайти: sin α і tg α, якщо cos α =7/25 і 3π/2 <α <2π
Другие вопросы по теме Математика
Популярные вопросы
- В каких случаях используется последний условный цикл (Информатика)...
3 - Дано F1=120 кн F2= 70 кн F3= 80 кн А1=16см2 А2=12см2...
3 - Вычисли столбиком и выполни проверку. 7306 400 - 503968 - 5471952 s.13 855100...
1 - Решите уравненияx^2:3x+1=03x^2:7x-6=0...
3 - просклоняйте слово Байтерек Менің сенің сіздің оның біздің сендердің сіздердің...
3 - 248. Спишите, подчеркните относительные имена прилагательные как члены предложения...
2 - Есе на тему „Чи можна не любити і росинку, і травинку, і дощову сльозинку?...
1 - 1) Соберите цепь, схема которой изображена на рисунке 8. Замкните цепь, снимите...
2 - В течении 9 минут через лампочку протекает электрический ток значение которого...
1 - Обчисліть масові частки всіх хімічних елементів у ферум (ІІІ) гідроксиді Fe(OH)3...
2
Пошаговое объяснение:
Основное тригонометрическое тождество: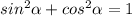
Выражаем из тождества синус: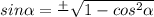 , причем знак перед корнем определяется тем, в какой четверти единичного круга находится угол
, причем знак перед корнем определяется тем, в какой четверти единичного круга находится угол 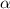 . Т.к. по условию 3π/2 <α <2π, то
. Т.к. по условию 3π/2 <α <2π, то 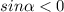 , =>
, =>