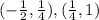Знайти інтервал зростання та спадання функції
f(x) = (x^2 + 2x)/4x-1
Другие вопросы по теме Математика
Популярные вопросы
- Какой корень в слове самостоятельный? !...
3 - Как записать цифрами два с половиной метра? зарание...
1 - Можете составить предложения с раздельным и слитнымнаписанием наголову...
3 - Розібрати за будовою прислівники: ближче, частіше...
3 - Sa preparat o solutue de 250 de gr.care contine 10 gr.de sare de bucatarie.calculati...
2 - По круговой дорожке бегут два спортсмена,скорость первого -12 км/ч,а...
2 - Найти цитаты из горе от ума по плану: 1. отношение к народу и крепостному...
1 - Разбери слова по составу: сахарница, выключатель, подлокотник, задвижка,...
1 - 10.наличие эвглены зеленой позволяет сделать : а.о сходстве живой и...
2 - Где обособленное обстоятельство? прежде чем сесть, валя снова оглянулась...
1
ответ: Увеличение на: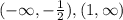
Убывает на: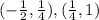 .
.
Пошаговое объяснение: Найдем производную.
Приравняем производную к 0.
Решим относительно x.
Упростим числитель.
Найдем НОЗ членов уравнения.
Умножим каждый член на и упростим.
и упростим.
Решим уравнение.
Разлагаем на множители левую часть уравнения.
Разделим обе части уравнения на 2. Результат деления 0 на любое ненулевое значение равен 0.
Приравняем x-1 к 0, затем решим относительно x.
Приравняем 2x+1 к 0, затем решим относительно x.
Решение является результатом x-1=0 и 2x+1=0.
Значения, которые обращают производную в 0 - 1,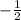 .
.
1,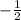 .
.
Выясним, при каких значениях переменной функция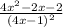 не определена.
не определена.
Разобьем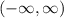 на интервалы вокруг значений x, в которых производная равна 0 или не определена.
на интервалы вокруг значений x, в которых производная равна 0 или не определена.
Подставим значение из интервала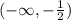 в производную, чтобы определить, возрастает или убывает функция.
в производную, чтобы определить, возрастает или убывает функция.
Увеличение на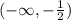 , так как
, так как 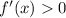 .
.
Подставим значение из интервала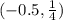 в производную, чтобы определить, возрастает или убывает функция.
в производную, чтобы определить, возрастает или убывает функция.
Убывает на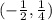 , поскольку
, поскольку 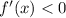
Подставим значение из интервала (0.25, 1) в производную, чтобы определить, возрастает или убывает функция.
Убывает на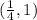 , поскольку
, поскольку 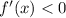
Подставим значения из интервала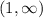 в производную, чтобы определить, возрастает или убывает функция.
в производную, чтобы определить, возрастает или убывает функция.
Увеличение на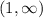 , так как
, так как 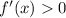 .
.
Перечислим промежутки, на которых функция возрастает и убывает.
Увеличение на: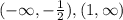
Убывает на: