Знайти границю використовуючи правило Лопіталя.
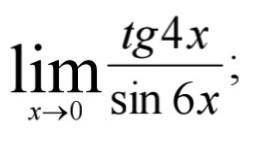
Другие вопросы по теме Математика
Популярные вопросы
- Закончи или дополни предложения, используя однородные члены. на небе сияли...
3 - Выражение и найти его значение 13 х+18х -х-5 при х=9...
1 - Обозначите орфограммы таких слов здоровая,большой,жители,вырыбатывается,полезный,арбузе,полезен,заболеваниях,плодоносное,растение,земле,собирать,год...
3 - Вкаком слове из этих примеров перед словом батьку должна стоять занятая?...
1 - Освободите от иррациональности знаменатель дроби 16_√8...
2 - Рассчитайте массовую долю каждого элемента в оксиде жедеза(3) и в оксиде...
1 - Напишите слова в которых происходит: c)оглушение согласных d) озвончение...
3 - 1)ab+3a 2) 5хy+5х 3) 3 хy- 6х 4) -6ab-15b...
2 - Синквейн на басню как мужик убрал камень ....
1 - Сочинение на тему жизнь маши троекуровой ! 20 !...
1
Находим производные: (tg4x)' =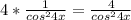 ;
;
(sin6x)' = 6*cos6x ⇒ исходный предел равен:
ответ: данный предел равен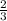
2/3
Пошаговое объяснение: