Знайти екстремуми функцій y= 2/3 x3 - 3/2 x2-9x
Другие вопросы по теме Математика
Популярные вопросы
- Расскажите о разных передачи чужой речи . придумайте примеры...
3 - Сообщение на тему заповедник ,заповедник можно выбрать любой...
2 - Дано n случайных чисел в диапазоне от -3 до 3. вычислите, сколько...
2 - Решите уравнение: 5/9x-2 1/3=; 14/39: x=24/52....
3 - Какие реликвии военных лет особенно дороги твоей семье...
1 - Найди и подчеркни в них дополнение.спина у меня заболела даже...
2 - Отправились,столкнулись какого времени...
3 - Вставить опребеления ехал илья муромец по какому полю?...
2 - Развернутый ответ на вопрос: почему мальчик не принял посылку?...
3 - Водной коробке 1/4 кг конфет, а в другой — на 1/5 кг больше....
1
2x²-3x-9=0 , D=90, x₁= , x₂=
, x₂= 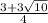
+ - +
y'_____( x₁)_____(x₂)_____
x₁= точка максимума
точка максимума
x₂=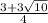 точка минимума
точка минимума