Знайдіть проміжки зростання і спадання та точки екстремуму функції y=x^2-3x/x+1
!!

Ответы

veder111oy2x71 16.06.2021 21:55

Чтобы найти промежутки возрастание/спадания функции и её экстремумы, нужно приравнять её производную к нулю:

$y = \frac{x^2-3x}{x+1}$

Найдём производную про правилу: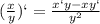 $(\frac{x}{y})`=\frac{x`y-xy`}{y^2}$ :

$y` = \frac{(x^2-3x)`(x+1)-(x+1)`(x^2-3x)}{(x+1)^2} = \frac{(2x-3)(x+1)-1(x^2-3x)}{(x+1)^2} =$

$= \frac{2x^2+2x-3x-3-x^2+3x}{(x+1)^2} = \frac{x^2+2x-3}{(x+1)^2}$

Приравняем производную к нулю:

$\frac{x^2+2x-3}{(x+1)^2} = 0$

Знаменатель не может быть равен нулю, значит приравняем к нему только числитель:

$x^2 + 2x - 3 = 0\\D = 2^2 - 4 * 1 * (-3) = 4 + 12 = 16\\\\x_1 = \frac{-2+4}{2} = 1\\\\x_1 = \frac{-2-4}{2} = -3$

Получили экстремумы функции.

Воспользуемся методом интервалов для нахождения промежутков возрастания и спадания функции. Т.к. возле старшего коэффициента стоит плюс, начинаем с плюса:

+ - +

-------(-3)----------(1)----------->

Функция возрастает на (-∞; -3] и [1; +∞)

Функция спадает на [-3; 1]

x = -3 - точка максимума

x = 1 - точка минимума

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика