Знайдіть проміжки зростання і спадання та точки екстремуму функції. Дочка тупица, я не лучше.
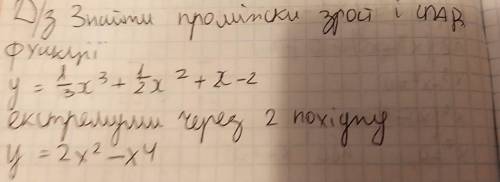
Другие вопросы по теме Математика
Популярные вопросы
- Рівння розв язати1) 6-3(x+1)=7-х...
3 - Ідейно художній аналіз твору захочеш- і будеш ...
1 - Present Simple or Present Continious Martin always (go) to the cinema on...
2 - Состваь предложения из слов. Выполни синтаксический разбор предложения выпиши...
3 - с задачей ) : Розвяжите задачу сложениям уравнения:Портфель тяжелее от чемодана...
3 - Накресліть прямокутний трикутник .За до транспортира,циркуля в лінійки побудуйте...
1 - Підготувати текстові запитання до творчо шляху О.Ольжича...
3 - X^2--16/x^2-8x+16=0 найти х...
1 - Які два океани спочає Панамський канал? географія...
3 - смену природных зон при движении от экватора к плюсам создовают?...
1
Пошаговое объяснение:
1. Промежутки возрастания и убывания функции:
y=x³/3+x²/2+x-2;
область определения функции - вся числовая ось. Фунция непрерывна при x∈(-∞;+∞)
попытаемся найти точки экстремума. Для этого возьмем производную:
y'=3x²/3+2x/2+1=x²+x+1;
приравняем производную к нулю:
y'=0; x²+x+1=0; D<0;
функция не имеет точек экстремума (максимума или минимума), т.е. функция монотонна на всей числовой оси (т.е. промежуток возрастания или убывания у функции один: x∈(-∞;+∞)).
Определим характер монотонности функции:
y=x³/3+x²/2+x-2;
x=0; y(0)=0+0+0-2=-2;
x=1; y(1)=1/3+1/2+1-2=(2+3)/6+1-2=11/6-12/6=-1/6;
x↑ y↑ - значение аргумента возрастает от 0 до 1, при этом значение функции также возрастает от -2 до -1/6. Следовательно функция монотонно возрастающая на всей числовой оси.
2.Определить экстремумы с й и 2-й производной.
y=2x²-x⁴;
возьмем первую производную:
y'=4x-4x³;
приравняем ее к нулю:
y'=0; 4x-4x³=0; 4x(1-x²)=0;
4x=0;
x₁=0;
1-x²=0; x²=1;
x₂=1; x₃=-1.
получаем три точки экстремума x₁=0;x₂=1; x₃=-1.
берем вторую производную:
y''=(4x-4x³)'=4-12x²;
подставляем в нее значения х₁, х₂, х₃:
y''(-1); y''(-1)=4-12*(-1)²=4-12=-8<0 - максимум
y''(0); y''(0)=4-0=4>0 -минимум
y''(1); y(1)=4-12*1²=-8<0 - максимум