1. Математика
  2. Знайдіть похідну dy/dx

Знайдіть похідну dy/dx функції, користуючись правилом логарифмічного диференціювання.
y=x^4^x

IAlisaI IAlisaI    2   19.12.2020 01:22    0

Ответы
1Дарина1234 1Дарина1234  12.02.2021 20:40

Пошаговое объяснение:

y=x^{4^x}

прологарифмируем обе части

lny=ln(x^{4^x})=4^xlnx

теперь продифференцируем

(lny)' = (4^xlnx)'

\frac{1}{y} y' = (4^x)'lnx +4^x(lnx)'

\frac{1}{y} y' = 4^xln4*lnx+4^x*\frac{1}{x} =4^x(ln4*lnx+\frac{1}{x} )

теперь вспоминаем, что у нас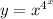    y=x^{4^x}   и  y'  это dy/dx получим требуемый ответ

\frac{dy}{dx} = x^{4^x}*4^x(ln4*lnx+\frac{1}{x} )

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
winterwhite123 winterwhite123  03.06.2019 11:40
Три загадки на татарском с отгадками...
steamlox1 steamlox1  03.06.2019 11:40
Вмузыкальном под первой (самой нижней)линейкой нотного стана стоит 1нота,на самой линейке 2ноты,между 1и 2линейками 3ноты,на второй линейке 4ноты,между 2 и 3 линейками 5нот...
катя5068 катя5068  03.06.2019 11:40
Есентябре количество теплых дней составило пять шестых долей месяца а в октябре таких дней было на 8 меньше. сколько всего было теплых дней в сентябре и октябре?...
Vankoed Vankoed  03.06.2019 11:40
Где алиса в стране чудес встречает чеширского кота?...
кавайнаятянка кавайнаятянка  03.06.2019 11:40
Запиши предложения в виде равенства: х в 8 раз меньше чем у а на 92 меньше чем b к в 5 раз больше чем d...
Ангелина545454 Ангелина545454  03.06.2019 11:40
Прогрессия (an) задана формулой аn = 3 * 2^n. какое из следующих чисел не является членом этой прогрессии: 1)24 2)72 3)192 4)384...
As337 As337  03.06.2019 11:40
От чего почва может растение...
MishaDunaev MishaDunaev  03.06.2019 11:40
Площадь одной двенадцатой части квадрата 3 см(2) найди площадь всего квадрата. начерти квадрат площадь которого равна площади прямоугольника со сторонами 2 см и 8 см. найди...
Ser099gei Ser099gei  03.06.2019 11:40
Слава принимал участие в забеге вместе с ещё 30-ю спортсменами. раньше славы при бежало в 4 раза меньше спортсменов чем прибежало после него. какое место занял слава?...
ЭМИР200720082009 ЭМИР200720082009  03.06.2019 11:40
Два стакана сока стоят 6 рублей. сколько стаканов сока можно будет купить на 6 рублей, если цена одного стакана снизится на 1 рубль.=?...

Популярные вопросы