Зная, что A,B,C внутренние углы треугольника- доказать справедливость равенств 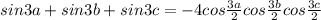
Другие вопросы по теме Математика
Популярные вопросы
- Белка. какие буквы согласных звуков какие гласных звуков...
1 - Площадь прямоугольника равна 36кв.см,а длины его сторон-натуральные...
3 - Решить систему уравнений 3х+5у=4, -3х+у=8...
3 - Написать на языке 8 предложений о том что надо делать чтобы поддержать...
3 - Оформите страничку календаря памятных дат ,посвящённую вашему земляку,который...
2 - Дзеркало рухається відносно землі зі швидкістю v . з якою швидкістю...
1 - Радиус движения тела по окружности уменьшилось в 2 раза, его линейную...
2 - Из данного предложения выпишите глагол ( глаголы ) || спряжения....
3 - Кто обитает только в азии выборы носорог слон жираф бегемот ванда...
2 - Повідомленя на тему деревій 5-7речень...
2
a+b+c=pi => sin(c)=sin(a+b)
sin(a)+sin(b)+sin(c)=sin(a)+sin(b)+sin(a+b)=2sin({a+b}/2)cos({a-b}/2)+2sin({a+b}/2)cos({a+b}/2)=2sin({a+b}/2)(cos({a-b}/2)+cos({a+b}/2))=
=2cos(c/2)*2*(cos(a/2)*cos(b/2)) что и требовалось доказать
sin({a+b}/2)=sin(90-c/2)=cos(c/2)