Зная что 3/4 от а равна 5/6 от в и 1/2 от с сравните а, в, а если а, в, с больше 0
Можно вы решите без системы мы её ещё не проходили
Другие вопросы по теме Математика
Популярные вопросы
- Решите уравнение : 0,2*(5у-2)=0,3*(2у-1)-0,9 !...
2 - Робин бобин барабек съел горячий чебурек, и цыпленка, и гуся, заливного...
3 - Решите ! в первый день бригада вспахала 2/9 поля, во второй день 3/18...
1 - Мешок картофеля тяжелее мешка с луком на 16 кг.сколько весит тот и...
1 - Заполнили водой два больших аквариума, в один они влили 300 л воды,...
3 - Кому приказал тимур разыскать пропавшую корову? 4 класс...
2 - Сочинение на тему зачем нужен циркуль...
3 - Сочинение государство юго западной азии...
2 - Уровнять методом электронного : ва (он)2+ н3ро4...
1 - Найдите рассказы где музыка играет главную роль...
2
ответ: b < a < c
Пошаговое объяснение:
1.
Рассмотрим это равенство. Домножим левую дробь на 6, правую - на 4, чтобы прийти к общему знаменателю:
Получим равенство (1), откуда следует, что b < a.
2.
Рассмотрим это равенство. Домножим правую дробь на 2, чтобы прийти к общему знаменателю:
Получим равенство (2), откуда следует, что a < c.
3. Теперь сравним c и b. Из равенства (2) возьмем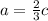 и подставим в равенство (1):
и подставим в равенство (1):
Домножим дробь при c на 6, чтобы прийти к общему знаменателю:
Откуда следует, что b < c.
Итак, мы получили следующее:
b < a
a < c
b < c
Откуда следует, что b < a < c.