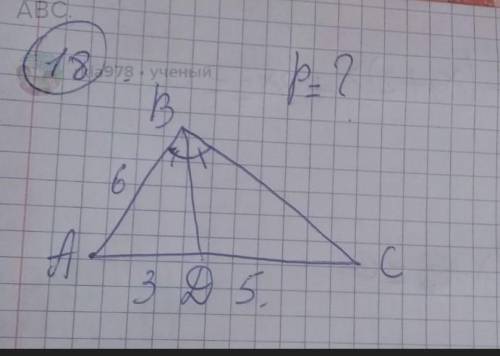
Знатоки математики ! BD-биссектриса. Найдите периметр АВС.

P=24

Пошаговое объяснение:

Пусть ∠ABC=∠α, ∠BDA=∠β - для удобства записи, IBCI=x

По теореме синусов для ΔABD:

3/sin(α/2) = 6/sinβ;                (1)

для ΔBDC, учитывая, что ∠BDC=180°- BDA=180-β (как смежные)

5/sin(α/2)=x/sin(180-β).        (2)

Немного алгебры:

из выражения (2)

5/sin(α/2)=x/sin(180-β) ⇔ x=5*sin(180-β)/sin(α/2)          (3)

                                            β≠180; α≠0 (хотя это и так ясно из условия)

из выражения (1)

3/sin(α/2) = 6/sinβ ⇔ sin(α/2)=3*sinβ/6=0,5*sinβ          (4)

подставляем  (4) в (3)

x=5*sin(180-β)/(0,5sinβ)

учитывая, что sin(180-β)=sinβ запишем:

x=5sinβ/(0,5sinβ)=5/0.5=10;

x=10

P=6+(3+5)+10=24