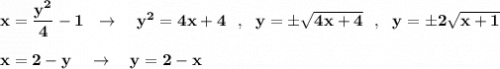Змінити порядок інтегрування в подвійному інтегралі.
Другие вопросы по теме Математика
Популярные вопросы
- Плоскость, параллельная основанию конуса, проходит через центр его высоты и...
1 - фото с заданием прикрепила...
1 - Знайди похідну даної функції y=4sinα+6ctgα−8arccosα....
3 - Яким я бачу майбутнє людства?...
2 - ПРОСТО СКАЖИТЕ ЧТО ПОДЧЕРКИВАТЬ И КАК(я не понимаю).. ...
3 - Знайти масу солі, яку потрібно додати до 400 грам води, щоб утворився 20% розчин...
3 - Суретте берілген эко жүйелер (А,В) түрлерін анықтаныз...
3 - Жаздыгүн шілде болғанда, Көгорай шалғын, бәйшешекҰзарып өсіп толғанда,Күркіреп...
2 - Наведить приклады экосистемы...
3 - Сколько раз совершит полный оборот колесо с диаметром 2,4 дм на пути длиной...
1
Изменить порядок интегрирования
Точки пересечения графиков :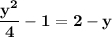 ,
,
Точки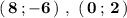 .
.
Выразим из уравнений линий у через х .