, желательно с объяснением
Задача по комбинаторике
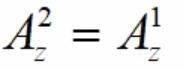
Другие вопросы по теме Математика
Популярные вопросы
- Начался ледоход на (лена,енесей,обь )записать без скобок...
1 - Составьте слово из пяти звуков, которые здесь описаны: 1) звонкий, парный...
2 - (6656: 512+28)•(1524: 127-7)-150 (4992: 384-8)•(8496: 236+15)+145...
2 - Углаголов получил, перепишу, лепит укажите форму времени. запиши каждый глагол...
2 - Однокоренные слова, называются паронимами...
3 - Эффективный диаметр молекулы газа 0,3 нм,давление газа 1 атм,температура...
2 - Решите уровнения. х+1620=12450-4980. у-1620=12450-4980. с-1620=12450+4980...
2 - Длина сторон треугольника равна 12см 5мм 4см 10см 5мм вырази длины сторон...
1 - Какие три основных цвета содержится в палитре для создания новых? a.жёлтый,серый...
3 - Какой объем воды получится, когда растает лед массой 900 кг, и температура...
3
Запись обозначает число размещений из
обозначает число размещений из  по
по 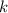 элементов. Имеет следующую формулу:
элементов. Имеет следующую формулу:
Решим уравнение. Помним, что z должно быть неотрицательным целым числом:
В конце делаем проверку, чтобы нигде не вылезли отрицательные факториалы.
P. S. Я решил эту задачу в уме секунд за 10, потому что помню формулу размещений и тот факт, что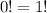 , а здесь
, а здесь 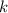 различается ровно на единицу.
различается ровно на единицу.