Желательно подробно ) И лайк

Другие вопросы по теме Математика
Популярные вопросы
- С ВОПРОСАМИ • Що дізналися Руснаки Руснаки про старовинну реліквію від...
2 - В каком году аккорда стала независимой...
1 - Исследование выталкивающей силы Тело длиной 10 см, площадью поперечного...
1 - Укажите продукты и составьте уравнения химических реакций a) K2CO3 + HNO3...
2 - Решите все эти задачи не отправлять ерунду и ошибочные ответы (флуд, спам...
3 - 4sin^2x+sinx×cosx+cos^2x=3cosx-cos3x=sin2x√2×cos3x×ctg3x-3√2×cos3x+ctg3x-3=0...
2 - Задача 3. Определите, как изменилась реальная заработная плата, если номинальная...
3 - 4. Плита, изготовленная из алюминия (р = 2,7 г/см3) имеет размер а = 12...
3 - У прямокутному трикутнику АКМ ( К=90°) АМ=45 см, cosM=0,7. Знайти катет...
3 - Сочинение-рассуждение на Лингвистическую тему по плану. 1.Существительное-...
1
(см. объяснение)
Пошаговое объяснение:
Рассмотрим сначала первое неравенство системы:
Видно, что левая его часть должна быть положительна. В свою очередь числитель дроби положителен. Это означает, что неравенство может быть верным только, если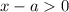 .
.
Тогда при домножении левой и правой частей неравенства на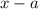 его знак сохранится.
его знак сохранится.
Получим эквивалентную систему:
Преобразуем ее до более удобного вида:
(данного результата можно было добиться также и приведением дроби к общему знаменателю; рассматриванием двух случаев; исключением одного)
Построим решения всех неравенств записанной выше системы в координатах (x; a):
(см. прикрепленный файл | выделено синим)
Рассмотрим вторую строку системы:
Преобразуем ее:
Приведем систему к более удобному виду:
Построим решения всех неравенств записанной выше фразы в координатах (x; a):
(см. прикрепленный файл | выделено фиолетовым)
Будем двигать горизонтальную прямую до тех пор, пока не добьемся требуемого результата.
(см. прикрепленный файл | выделено оранжевым)
Тогда понятно, что достаточно решить систему:
Откуда следует, что при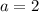 исходная система неравенств имеет единственное решение
исходная система неравенств имеет единственное решение 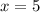 .
.
Задание выполнено!