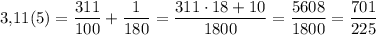Завтра экзамен! решите с решением! 1) представить бесконечную периодическую дробь в виде обыкновенной: 1) 0,(35); 2) 3,11(5).
Другие вопросы по теме Математика
Популярные вопросы
- Какова причина электрического сопротивления внутри батарейки?...
2 - Подскажите как решить эти уравнения: 3(x+6)=x+2(x+9) и ещё: 2(8x-7)=18-(5-4x)...
3 - По какому признаку растения объединяют в одно семейство? 1) один и тот же...
2 - Придумайте, как очистить каспийское море, восстановить флору и фауну, замотивировать...
3 - Вшаре на расстоянии 15 см от центра проведено сечение радиус, которого 8 см....
3 - При делении данного числа n на 225 в остатке получилось 150. разделится ли...
2 - Смесь бутана с пропаном как называется?...
2 - Не могу понять : с линейки и транспортира постройте треуголник ,две стороны...
1 - Площадь сечения прямого цилиндра равна 540см^2, а радиус равен 9см. найти...
3 - Вопросы с фразы всё вернётся с ответами...
3
1)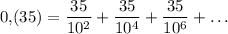
Правая часть равенства представляет собой бесконечно убывающую геометрическую прогрессию, где первый её член равен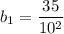 , а знаменатель
, а знаменатель 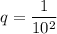
Формула суммы бесконечно убывающей геом. прогрессии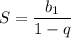
Значит,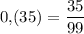
2)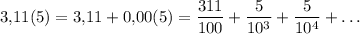
Аналогично примеру в пункте (1), для периодической дроби в правой части уравнения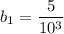 и
и 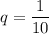
Значит,