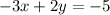Запишите уравнение прямой ax+by=c ( где a,b,c целые числа), проходящей через точки М( 1;-1) N(3;2)
Другие вопросы по теме Математика
Популярные вопросы
- А) имеются ли среди чисел 2! , 3! , 4! , 5! , 6! , 7! , взаимно простые числа?...
2 - Образуй от слов-предметов слова-действия....
2 - Mn(m- во 2 степяни -n во 2 степяни )(2m+n)...
3 - 1. в одном равнобедренном треугольнике угол при вершине равен 24 градусов, а...
2 - Решить с подробным объяснением: для приготовления ванны вместимостью 200 л смешали...
2 - Туристи каждий день по 5 банок консервов. сколько банок консервов туристи за...
3 - Зачем моисей водил евреев 40 лет по пустыни?...
1 - По какому принципу название деревьев распределили на 2 группы? 1)клён,кедр,вяз,ель,дуб...
1 - Написать предложение для каждого слов / фраз (at the momenr), ( on sundays )...
2 - На рисунке изображена сложная замкнутая ломаная. она ограничивает некоторую...
3
Если данная прямая проходит через точки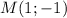 и
и 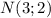 , то получим систему уравнений:
, то получим систему уравнений:
Помимо этого, через точку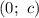 прямая тоже должна пройти — точка пересечения прямой с осью ординат. Таким образом, получили систему трех уравнений:
прямая тоже должна пройти — точка пересечения прямой с осью ординат. Таким образом, получили систему трех уравнений:
Вычтем из первого уравнения второе уравнение:
Тогда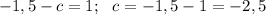
Получили уравнение прямой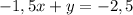
Так как по условию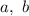 и
и  — целые числа, домножим получившееся уравнение на 2:
— целые числа, домножим получившееся уравнение на 2:
ответ: