1. Математика
  2. Запишите комплексное число в

Запишите комплексное число в алгебраической и тригонометрической формах 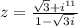z=\frac{\sqrt{3}+i^{11} }{1-\sqrt{3i} }

natava1998 natava1998    3   29.06.2021 17:16    0

Ответы
Sheria777 Sheria777  29.07.2021 17:41

z=\frac{\sqrt{3}+i^{11}}{1-i\sqrt{3}}=?\\\\i^{11}=i^{10}*i=((i^2)^5)*i=(-1)^5*i=-1*i=-i\\\\\ z=\frac{\sqrt{3}+i^{11}}{1-i\sqrt{3}}= \frac{\sqrt{3}-i}{1-i\sqrt{3}}=\frac{(\sqrt{3}-i)(1+i\sqrt{3})}{(1-i\sqrt{3})(1+i\sqrt{3})}=\frac{\sqrt{3}-i+i(\sqrt{3})^2-i^2\sqrt{3}}{1^2-(i\sqrt{3})^2}=\frac{\sqrt{3}-i+3i+\sqrt{3}}{1+3}=\\\\=\frac{2\sqrt{3}+2i}{4}=\frac{\sqrt{3}}{2}+\frac{1}{2}i

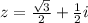Итак, \\\\z=\frac{\sqrt{3}}{2}+\frac{1}{2}i - это  алгебраическая форма комплексного числа.

Теперь найдём его тригонометрическую форму:

a=\frac{\sqrt{3}}{2};b=\frac{1}{2}\\\\|z|=\sqrt{a^2+b^2}=\sqrt{\frac{(\sqrt{3}}{2})^2+(\frac{1}{2})^2}=\sqrt{\frac{3}{4}+\frac{1}{4}}=\sqrt{1}=1\\\\(cos\psi=a/|z|= \frac{\sqrt{3}}{2};sin\psi=b/|z|= \frac{1}{2})=\psi=\pi /6\\\\z=|z|(cos\psi+isin\psi)\\\\z=1(cos\pi /6+isin\pi /6)\\\\\ z=cos\pi /6+isin\pi /6}

Это тригонометрическая форма числа z

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Zabuzamomochiiii Zabuzamomochiiii  17.11.2020 09:23
Определи первые пять членов последовательности (xn), заданной рекуррентно: x1=−6, xn=xn−1+7, n=2,3,4... ответ: x2= ;x3= ;x4= ;x5= ....
7гогого7896шол 7гогого7896шол  17.11.2020 09:24
Нужна с не очень сложной задачей.Всё на фото.( )...
69Unicorn69 69Unicorn69  17.11.2020 09:24
Построить графики Найти к, в.БЫСТРЕЕ...
michlich michlich  17.11.2020 09:31
Проклассифицируйте вещества на органические и неорганические: крахмал, глюкоза, вода,пищевая сода, гемоглобин,углекислый газ, кислород, фруктоза,железо, лактоза, целлюлоза, кислород.​...
lera956 lera956  17.11.2020 09:31
(х-80):40=640 (х-80):40=640 х-80=640:40 х-80=640:40...
artgensh artgensh  17.11.2020 09:31
При каком значении а система имеет бесконечное множество решений?...
тто тто  17.11.2020 09:31
8 КИБ = 65 536 бит ( З 145 728 МИБ = ГИБ...
Elizabetsimmer Elizabetsimmer  17.11.2020 09:31
найди три следующих числа в последовательности. 1/13; 3/13; 5/13; МОЖНО БЫСТРЕЕ ​...
никита42728 никита42728  17.11.2020 09:31
Найди значение выражения 5 / 12 + 3 / 4 + 7 / 12...
innocen innocen  17.11.2020 09:31
Көмек беріңдерші өтінемін​...

Популярные вопросы