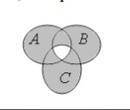
Записать выражение для множества, изображенное ниже с диаграмм Эйлера-Венна

На данной диаграмме Эйлера-Венна изображено множество, состоящее из трех подмножеств: A, B и C. Для записи этого множества в форме выражения, мы будем использовать обозначения теории множеств.

Мы начнем с определения каждого из подмножеств на диаграмме:

A - это множество элементов, которые находятся внутри первого круга на диаграмме. В данном случае, мы видим число 1 и 2 внутри этого круга.

B - это множество элементов, которые находятся внутри второго круга на диаграмме. Здесь мы видим число 2, 3 и 4.

C - это множество элементов, которые находятся внутри третьего круга на диаграмме. В данном случае, мы видим число 3.

Теперь мы можем записать это множество с использованием обозначений теории множеств.

A = {1, 2}
B = {2, 3, 4}
C = {3}

Теперь мы можем записать множество, объединяя все подмножества с использованием операции объединения (обозначается символом U).

Таким образом, запись множества на данной диаграмме будет выглядеть следующим образом:

A U B U C = {1, 2} U {2, 3, 4} U {3}

Здесь мы объединяем все элементы из подмножеств A, B и C, и получаем полное множество элементов изображенных на диаграмме.

Таким образом, полученное множество будет содержать элементы: 1, 2, 3 и 4.