Записать уравнение окружности, которое проходит сквозь указанные точки и имеет центр в точке Фокуси гіперболи 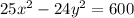, A(0, -8)

Пошаговое объяснение:

сначала запишем каноническое уравнение гиперболы

для этого поделим всё на 600

отсюда получим вещественную полуось a=√24, и мнимую b=√25=5.

теперь расстояние от начала координат до каждого из фокусов c соотносится с полуосями как

с² = а² + b² = 24 + 25 = 49  ⇒ с = ±7

т.е. мы нашли координаты фокусов F₁ = (-7; 0)   F₂ = (7; 0)

теперь у нас есть центр и значит мы можем вычислить радиус как расстояние между точкой и центром окружности

R² = d² = (0-7)² + ((-8) +0)² = 49 + 64 = 113

вот и всё. уравнение окружности

(x-0)² +(y+8)²=113

x² +(y+8)² = 113