Записать множества А, B, C с перечислением их элементов и найти , , , , если А – множество делителей числа 12, В – множество корней уравнения , С – множество нечетных чисел , таких что
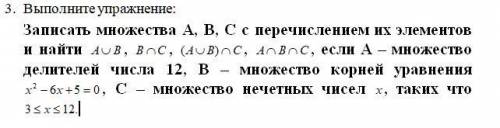
Ответы
Вопрос просит записать множества А, В и С с перечислением их элементов, а затем найти несколько операций над ними. Давайте начнем с определения каждого множества и нахождения его элементов.
Множество А - множество делителей числа 12:
Делители числа 12 - это числа, на которое 12 делится без остатка. В данном случае, делители числа 12 - это числа, на которое 12 делится без остатка и которые меньше или равны 12.
Итак, для определения множества А нам нужно найти все числа, на которые 12 делится без остатка. Эти числа будут элементами множества А. Возможные делители числа 12 - это числа: 1, 2, 3, 4, 6 и 12.
Таким образом, множество А = {1, 2, 3, 4, 6, 12}.
Множество В - множество корней уравнения:
Для определения множества В, нам нужно найти все значения корней уравнения . Однако, данного уравнения для нас не видно в тексте. Необходимо проверить, является ли такое уравнение заданным или это опечатка.
Множество С - множество нечетных чисел, таких что
Для определения множества С, нам нужно найти все нечетные числа, которые удовлетворяют заданному условию .
Условие говорит о том, что нечетные числа должны быть строго больше 1 и строго меньше 7. Поэтому, все нечетные числа, которые удовлетворяют этому условию, будут элементами множества С.
Подведем итоги:
Множество А = {1, 2, 3, 4, 6, 12}
Множество В - не определено из-за отсутствия уравнения.
Множество С = {3, 5}
Следующая часть вопроса требует нахождения нескольких операций над множествами А, В и С. Нам нужно найти следующие значения: , , , , .
Обратите внимание, что операция "+" означает объединение множеств, а операция "-" означает разность множеств.
1. Найдем объединение множеств А и С.
Множество А + С = {1, 2, 3, 4, 6, 12} + {3, 5} = {1, 2, 3, 4, 5, 6, 12}
Объединение множеств А и С содержит все элементы обоих множеств: {1, 2, 3, 4, 5, 6, 12}.
2. Найдем пересечение множеств А и С.
Множество А ∩ С = {1, 2, 3, 4, 6, 12} ∩ {3, 5} = {3}
Пересечение множеств А и С содержит только общий элемент у них: {3}.
3. Найдем разность множеств А и С.
Множество А - С = {1, 2, 3, 4, 6, 12} - {3, 5} = {1, 2, 4, 6, 12}
Разность множеств А и С содержит все элементы множества А, которые не принадлежат множеству С: {1, 2, 4, 6, 12}.
4. Найдем дополнение множества А.
Дополнение множества А - это все элементы, которые не принадлежат множеству А и содержатся в универсальном множестве. В данном случае, универсальное множество не указано, поэтому необходимо либо предположить, что это множество всех целых чисел, либо обратиться за уточнением к автору вопроса.
В итоге, множества А, В и С состоят из следующих элементов:
Множество А = {1, 2, 3, 4, 6, 12}
Множество В - не определено из-за отсутствия уравнения.
Множество С = {3, 5}
Операции над множествами:
1. Множество А + С = {1, 2, 3, 4, 5, 6, 12}
2. Множество А ∩ С = {3}
3. Множество А - С = {1, 2, 4, 6, 12}
4. Дополнение множества А - не указано без уточнения универсального множества.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Популярные вопросы
- дайте определения этим терминам: Великое переселение народов Феодальное поместье....
1 - Краткий пересказ произведения княжна джаваха чень краткий ну ёмаё...
3 - Как возвести в квадрат? (ФСУ) С объяснением (что, откуда, как)...
2 - Hey, Manuscript Alli sent you a message. To reply, go directly to the conversation...
1 - Кубинская резня Лезгин. объясните что произошло…...
3 - Рух точки задано рівняннями x=4t^2, y=2+3t^2 . Знайти рівняння траєкторії точки,...
2 - В параллелограмме ABCD угол BAD равен 60 градусов, а биссектриса этого угла делит...
2 - Вычислите значение выражения (5^3*5^-4)^2 1)1/5 2)5 3)1/25 4)25...
2 - 1. Sandy (read) history books daily. 2. What is Lisa doing now? - Lisa (write)...
3 - . высота проведенная из вершины тупого угла равнобедренной трапеции, делит ее...
3