Запись девятизначного числа, делящегося на 37, разделили на две части и переставили
эти части друг с другом. обязательно ли полученное девятизначное число будет делиться
на 37 ? (конечно, с пояснениями, а не один ответ).
Другие вопросы по теме Математика
Популярные вопросы
- Чему равна скорость автомобиля если за 30 минут проедет 72 км...
1 - Найдите вероятность того, что после двух бросков правильной монеты...
1 - Опишите традицию которая соблюдается в вашей семье на каких ценностях...
2 - Тело на пружине колеблеться вдоль вертикали,при этом длина пружины...
2 - Электрическое напряжение на концах участка цепи каким выражением...
3 - Найди значение m, если: а)-m=8; b)-m=-18. c)-m=0...
2 - Установіть відповідність між назвами держав та українськими землями,...
1 - Критмической закономерности развития оболочки относится...
2 - Придумать стихотворение. скиньте какое-нибудь стихотворение 6-8 строк,...
3 - Преимущества и недостатки спорта, с переводом на . , хелп ми....
1
Пусть наше число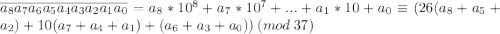
Тогда после перестановок могут получиться числа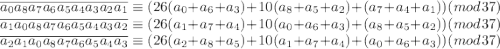
Как можно заметить, каждое из этих чисел сравнимо по модулю 37 с одним из трех чисел: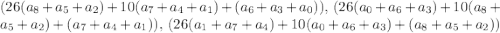
Обозначим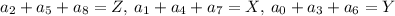
Тогда, по условию,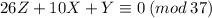
Заметим, что сумма этих трех возможных остатков равна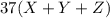 , а значит кратна 37. Тогда, если
, а значит кратна 37. Тогда, если 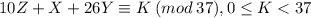 , то
, то 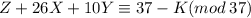
Значит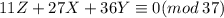
Тогда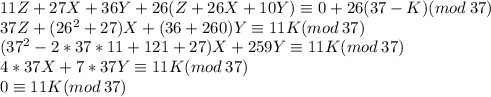
А значит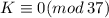 . Тогда, с учетом ограничений,
. Тогда, с учетом ограничений, 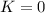 .
.
А значит все числа, получающиеся с таких перестановок, кратны 37.
ответ: Да