1. Математика
  2. Задумали 17 целых чисел.

Задумали 17 целых чисел. оказалось что сумма задуманных чисел равна 125. после чего каждое число изменили: либо разделили его на 3, либо умножили его на 5. могла ли сумма полученных чисел 17 чисел равняться 175?

Рокистка068 Рокистка068    3   24.01.2020 19:58    4

Ответы
Nikita6537 Nikita6537  11.10.2020 03:03

Пусть сумма чисел, которые разделили на 3, равна A, а тех, которые умножили на 5, равна B.

Тогда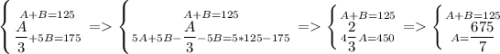 \left \{ {{A+B=125} \atop {\dfrac{A}{3}+5B=175}} \right. = \left \{ {{A+B=125} \atop {5A+5B-\dfrac{A}{3}-5B=5*125-175}} \right. = \left \{ {{A+B=125} \atop {4\dfrac{2}{3}A=450}} \right. = \left \{ {{A+B=125} \atop {A=\dfrac{675}{7}}} \right.

A не целое. С другой стороны, A - сумма целых чисел. Противоречие. А значит такого быть не могло

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
ЛИЗАЛАРИНА ЛИЗАЛАРИНА  18.05.2021 21:47
Решите ,очень надо,1 вариант(7не надо)...
TemhenkoShasa TemhenkoShasa  18.05.2021 21:47
Три бригады за смену изготовили 58 деталей. Преврая брегада изготовила на 10 деталий меньше чем, вторая, а третья- 0,5 деталий, изготовленных первой и второй брегадой...
Artishokq Artishokq  18.05.2021 21:45
Постройте на координатной плоскости точки: А(-6;3); В(3;0); С(-2;1); D(1;-2). а) Проведите прямые АВ и СD. б) Найдите координаты точек пересечения: прямых АВ и СD;...
abeloglazova891 abeloglazova891  18.05.2021 21:44
Решите уравнение! 12,2+(−x)=−2 4/5.(2 целых 4/5)....
visnevsk visnevsk  18.05.2021 21:44
Вычислите длину окружности, если её радиус равен 4,1см....
apetrochenkov apetrochenkov  18.05.2021 21:44
-4(6-2a)-2(a-8)+8 упростите выражение .​...
Lutiypacan1437 Lutiypacan1437  18.05.2021 21:44
(86 102 - 83 602): 500 - 354 + 64 • 105 27- 235 • 72) • 2504 - 19 008 : 36 сколько (( ​...
viktoriyabolgova viktoriyabolgova  18.05.2021 21:43
дайте ответ мне надо Бистра щяс ноч я сижу в школе​ сори я нечайно поставил матем это музыка...
kozlovavika200 kozlovavika200  18.05.2021 21:42
Для покраски лавочек в парке было куплено 45 банок синей краски по 5 кг и 60 банок зелёной краски по 3 кг. Сколько всего килограммов краски было куплено? составить...
Strellerts Strellerts  18.05.2021 21:42
Есть два соседних круга. Расстояние d между центрами двух окружностей составляет 16 см. Если их радиусы пропорциональны 5 и 3 цифрам, каков их радиус? Расмотрите ответ...

Популярные вопросы