Задания из высшей математики вычислить производную.

Другие вопросы по теме Математика
Популярные вопросы
- 10,12,4,7,2,5,1,8,11, 3 ,9, 6 пиши всё по порядку как я тебе написал) удачи...
1 - Выражение 2целых 2/3 а + 1 целая 1/6 а...
1 - Морфологические разбор наличия когда-то...
3 - Как назаваются водные объекты нашего края?...
2 - Образ героя комедии недоросль наиболее удачно созданным фонвизиным...
1 - Прочитайте вопросы и подготовьте на них вопросы...
1 - 5решите сколько будет если 5+5=10+10=30...
3 - Знайти значення виразив округлення. 5+7...
3 - Translate the following (a) using ‘little’, ‘a little’, ‘few’, ‘a few’*:...
1 - Какое из этих утверждений ошибочное? 1 краткие прилагательные являются...
1
Воспользуемся следующими правилами и формулами дифференцирования:
Воспользуемся следующими правилами и формулами дифференцирования:
Воспользуемся следующими правилами и формулами дифференцирования:
Воспользуемся следующими формулами дифференцирования:
В формулах и правилах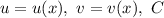 — постоянная.
— постоянная.