Задана функция 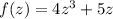Найти:
a) значение этой функции в точке z₀= -1+i
б) значение её производной в точке z₀= 1+2i

Для решения этой задачи нам нужно использовать формулу вычисления значения функции в заданной точке и формулу вычисления производной функции. Давайте начнем с пункта а).

a) Значение функции в точке z₀= -1+i:
Для вычисления значения функции в заданной точке, нам нужно подставить значение этой точки вместо переменной в функцию.

Итак, функция f(z)= 4z³ + 5z.
Мы должны найти значение этой функции в точке z₀= -1+i.
Заменяем z в функции на z₀:
f(z₀) = 4z₀³ + 5z₀.
Подставляем значение z₀= -1+i:
f(z₀) = 4(-1+i)³ + 5(-1+i).

Теперь давайте разберемся с вычислением значения функции в этой точке. Возводим (-1+i) в куб:
(-1+i)³ = (-1+i)²(-1+i) = (-1+2i-i²)(-1+i) = (1-2i+i²)(-1+i).
Заметим, что i² = -1, поэтому можно заменить i² на -1:
(1-2i+i²)(-1+i) = (1-2i+(-1))(-1+i) = (0-2i)(-1+i).
(0-2i)(-1+i) = -2i+2i² = -2i+2(-1) = -2i-2 = -2(1+i).

Теперь мы можем продолжить расчет, подставив данный результат обратно в исходную функцию:
f(z₀) = 4(-1+i)³ + 5(-1+i) = -2(1+i) + 5(-1+i).

Теперь упростим это выражение:
-2(1+i) + 5(-1+i) = -2-2i-5+5i = -7+3i.

Таким образом, значение функции в точке z₀= -1+i равно -7+3i.

б) Значение производной функции в точке z₀= 1+2i:
Для вычисления значения производной функции в заданной точке, нам следует применить формулу для вычисления производной функции.

Итак, функция f(z)= 4z³ + 5z.
Мы должны найти значение производной этой функции в точке z₀= 1+2i.
Производная функции f(z) находится путем дифференцирования функции по переменной z, то есть мы должны найти f'(z).

Вычисляем производную функции, применяя правило дифференцирования степенной функции и линейной функции:
f'(z) = (4 * 3z²) + 5 = 12z² + 5.

Теперь мы можем подставить значение z₀= 1+2i в найденную формулу производной:
f'(z₀) = 12(1+2i)² + 5.

Раскроем скобки и получим:
(1+2i)² = 1+4i+4i² = 1+4i+4(-1) = 1+4i-4 = -3+4i.

Теперь продолжаем вычисление:
f'(z₀) = 12(-3+4i) + 5 = -36+48i + 5.

Упростим это выражение:
-36+48i + 5 = -31+48i.

Таким образом, значение производной функции в точке z₀= 1+2i равно -31+48i.