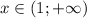Задана функция f(x)=x^3-3x^2-24x-28 найти экстремумы и точки перегиба. ,
Другие вопросы по теме Математика
Популярные вопросы
- Вычисли.11 -11 +11 -11 +2Верных ответов: 2...
1 - 1. Скільки полків налічувалось в Українській гетьманській державі? а)...
2 - Какие факторы определяли положение США после второй мировой войны?(Коротко...
1 - Купили 4 пирожка с вишней по 9 р. и 5 пирожков с творогом по 10 р. Сколько...
3 - 2. Какими были основные слои населения украинских земель в первой полови-не...
1 - Найти ускорение свободного падения на планете Y. масса которой равна...
2 - ДАЙТЕ ПРАВИЛЬНЫЙ ОТВЕТ УМОЛЯЮ только правильный!...
3 - Перемоги героїв в оповідання Останній Дюйм Напишите...
3 - 2) Игрушечный автомобиль массой 200г движется по горизонтальной поверхности...
3 - Разложите многочлен:a2-4-a-2...
1
Пошаговое объяснение:
Методом интервалов находим, что
Находим, что
Находим точки перегиба, для этого:
График функции выгнут при
при 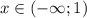
График функции вогнут при
при