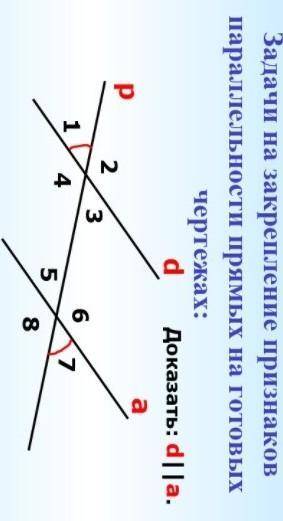
Задачи на закрепление признаков параллельности прямых на готовых чертежах: Доказать: d||a.​

Привет! Я с удовольствием помогу тебе с этой задачей.

Для доказательства параллельности прямых d и a на данном чертеже, нам понадобится использовать несколько признаков параллельности.

Первый признак параллельности прямых, который мы можем использовать, основан на свойствах углов. Этот признак утверждает, что если две прямые параллельны, то углы, образованные их пересечением с другой прямой, равны между собой.

На нашем чертеже мы можем найти несколько углов, образованных прямыми d и a с третьей прямой, обозначенной как b. Давай их обозначим.

Угол 1 образован прямыми d и b.
Угол 2 образован прямыми a и b.
Угол 3 образован прямыми d и a.

Теперь, чтобы доказать, что d||a, нам нужно показать, что угол 3 равен углу 2. Если это будет верно, то это будет означать, что прямые d и a параллельны.

Для этого нам понадобится использовать свойство смежных углов. Свойство смежных углов утверждает, что если угол 1 и угол 2 являются смежными углами, то их сумма равна 180 градусов.

В нашем случае угол 1 и угол 2 являются смежными углами, так как оба они образованы прямой b. Значит, их сумма должна быть равна 180 градусов.

Теперь смотрим на наш чертеж и измеряем уголы 1 и 2 с помощью градусного треугольника или другого инструмента для измерения углов. Давай обозначим эти значения как угол 1 = x градусов и угол 2 = y градусов.

Если x + y = 180, то это будет означать, что угол 1 и угол 2 являются смежными углами и их сумма равна 180 градусов. А это уже доказывает, что d и a параллельны.

Надеюсь, это понятно! Если у тебя есть еще вопросы, не стесняйся задавать их мне.