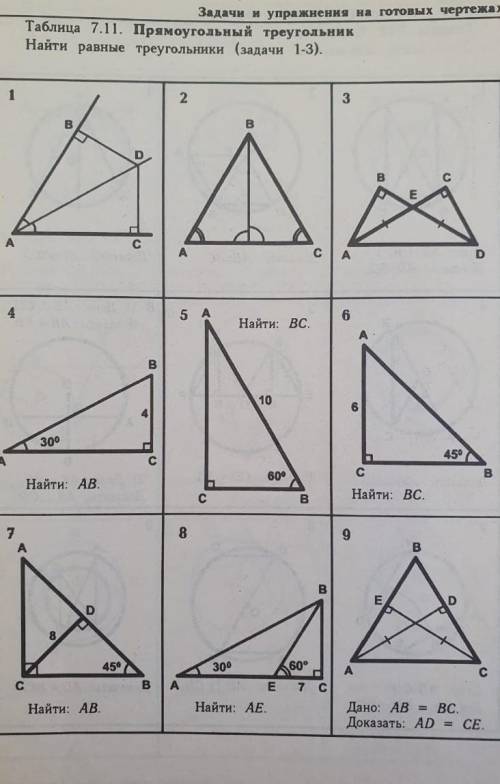
Задачи и уравнения на готовых чертежах таблица 7.11 прямоугольный треугольник

Добрый день! Рад, что вы обратились ко мне со своим вопросом. Давайте разберем его пошагово.

На данном чертеже видно, что есть прямоугольный треугольник ABC, в котором у нас есть два катета - AC (вертикальная сторона) и BC (горизонтальная сторона), а также гипотенуза AB (наклонная сторона).

Итак, давайте рассмотрим задачи и уравнения, связанные с этим прямоугольным треугольником.

1. Найти длину гипотенузы AB.

Для решения этой задачи мы можем использовать теорему Пифагора, которая говорит, что сумма квадратов длин катетов равна квадрату длины гипотенузы:

AC^2 + BC^2 = AB^2.

В данном случае, мы знаем значения катетов: AC = 5 см и BC = 12 см. Подставляем эти значения в уравнение и решаем:

5^2 + 12^2 = AB^2,
25 + 144 = AB^2,
169 = AB^2.

Чтобы найти значение AB, нужно извлечь квадратный корень из 169:

AB = √169,
AB = 13 см.

Итак, длина гипотенузы AB равна 13 см.

2. Найти длину катета AC.

В данной задаче, нам нужно найти длину вертикального катета AC. Для этого мы можем использовать теорему Пифагора и уже известную длину гипотенузы AB:

AB^2 = AC^2 + BC^2.

Мы уже знаем, что AB = 13 см, а BC = 12 см. Подставляем эти значения и решаем уравнение:

13^2 = AC^2 + 12^2,
169 = AC^2 + 144,
169 - 144 = AC^2,
25 = AC^2.

Чтобы найти значение AC, нужно извлечь квадратный корень из 25:

AC = √25,
AC = 5 см.

Итак, длина вертикального катета AC равна 5 см.

3. Найти угол ABC.

Для нахождения угла ABC мы можем использовать функцию тангенс. Тангенс угла определяется как отношение противолежащего катета (вертикального катета AC) к прилежащему катету (горизонтальному катету BC):

тангенс угла ABC = AC / BC.

Подставляем известные значения:

тангенс угла ABC = 5 / 12.

Теперь нам нужно найти обратный тангенс этого значения (используйте калькулятор или таблицу обратного тангенса). Обозначим это значение как θ (тета):

θ = arctan(AC / BC).

Вычисляем:

θ = arctan(5 / 12).

Теперь используя калькулятор или таблицу обратного тангенса, мы получаем значение угла ABC:

θ ≈ 0.41 радиан или примерно 23.6 градусов.

Итак, угол ABC примерно равен 23.6 градусов.

Вот и все! Мы разобрали задачи и уравнения на готовом чертеже прямоугольного треугольника. Если у вас возникнут еще вопросы, не стесняйтесь задавать их.