Задача на теория вероятности где-то 11 класс. Идёт зачёт по обществознанию, всего 9 билетов. Каждый ученик из класса

Question

Математика: Задача на теория вероятности где-то 11 класс. Идёт зачёт по обществознанию, всего 9 билетов. Каждый ученик из класса подходит к учителю и вытягивает билет, если попался билет, который он не знает, то ему даётся 2-ая попытка, при этом первый билет, который вытянул этот ученик, убирается (их становится на 1 меньше). Всего у ученика есть 3 попытки(за каждую попытку снимается ). На последней попытке, т.е. 3-ей, билетов становится 7 штук. Вася выучил всего 2 билета, и он утверждает, что шанс того, что

kirrilkyplenow · Answer

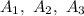Пусть случайное событие — хотя бы один раз попадется нужный билет. Тогда события $A_{1}, ~ A_{2}, ~ A_{3}$ — попался нужный билет с первой, второй, третьей попытки соответственно.

Вероятность наступления событий $A_{1}, ~ A_{2}, ~ A_{3} \colon$

$P(A_{1}) = \dfrac{2}{9}; ~~~ P(A_{2}) = \dfrac{2}{8}; ~~~ P(A_{3}) = \dfrac{2}{7}.$

Поскольку события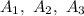 $A_{1}, ~ A_{2}, ~ A_{3}$ независимы в совокупности, а событие означает, что случилось хотя бы одно из этих событий, то

$P(A) = 1 - (1 - P(A_{1}))(1 - P(A_{2}))(1 - P(A_{3})) = \\= 1 - \left(1 - \dfrac{2}{9} \right)\left(1 - \dfrac{2}{8} \right)\left(1 - \dfrac{2}{7} \right) = 1 - \dfrac{7}{9} \cdot \dfrac{6}{8} \cdot \dfrac{5}{7} = \dfrac{7}{12} \approx 0,58.$

Следовательно, шанс того, что Васе попадется нужный ему билет больше 50%.

ответ: да, прав.

Популярные вопросы