Задача №7. Заданную функцию y = f (x) исследовать на непрерывность и выяснить характер точек разрыва. Сделать схематический график
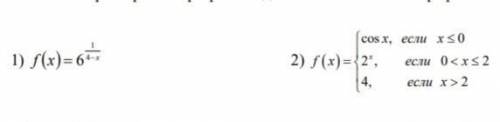
Другие вопросы по теме Математика
Популярные вопросы
- Космический корабль после полета...
3 - Тело весом P=800H равномерно подняли на небольшую высоту за время,равное t=12c....
2 - Добери і запиши синоніми до слів темрява,постривайте,заприятелюємо...
1 - Водная среда характеризуется достаточным ко-личеством…………. Температура ……….не...
3 - Написать 10 пунктов сравнения горный пород...
3 - Установите, какие ошибки допущены в данных предложениях, классифицируйте их. Предложите...
2 - Стіл 7 дм а табуретка 3 дм на скільки дм табуретка нижча за стіл?...
3 - надо всё сделать что на фото...
2 - Тест по немецкому теме Mein Schultag Выбрать верный вариант ответа. 1. … Montag,...
1 - Даны вещества: Cu, S, O2, H2, CuO. Напиши уравнения реакций между веществами,...
1
1. f(a) - значением функции в точке a существует
2. lim(x→a) f(x) - предел функции при x стремящемся к a существует
3. f(a) = lim(x→a) f(x) - предел функции равен значению функции в точке a
Теперь приступим к исследованию непрерывности функции y = f(x) из задачи:
1. Проверим существование значений функции в заданных точках.
a) При x < -4 функция не определена, так как указано, что f(x) = √(x+4) и x+4 не может быть отрицательным числом, поэтому в данном случае функция не существует.
б) При x ≥ -4 функция существует и равна √(x+4).
2. Проверим существование предела функции при x стремящемся к заданным точкам.
a) Проверим предел при x → -4. Подставим x = -4 и найдем предел: lim(x→-4) √(x+4) = √(0) = 0. Значит, предел существует.
б) Проверим предел при x → ∞. Для этого рассмотрим поведение функции при x, стремящемся к бесконечности. При больших положительных x, √(x+4) будет стремиться к бесконечности. Значит, предел при x → ∞ не существует.
3. Проверим выполнение условия равенства значения функции и ее предела в заданных точках.
a) Проверим f(-4) = lim(x→-4) √(x+4). Значение функции в точке -4 равно 0, как мы уже выяснили ранее. Предел функции при x → -4 также равен 0. Поэтому условие равенства значений и пределов выполняется.
Таким образом, функция y = f(x) непрерывна при x ≥ -4 за исключением точки x = -4, где имеется устранимый разрыв.
Теперь перейдем к построению схематического графика функции:
1. Начнем с осей координат. Поскольку функция существует только при x ≥ -4, мы будем рисовать график только после этой точки и справа от нее.
2. Строим график функции √(x+4). Поскольку при x = -4 имеется устранимый разрыв, мы рисуем открытую точку в этой точке, чтобы показать, что функция не определена здесь. При x ≥ -4 график функции будет растущей кривой, направленной вверх.
Таким образом, построен график функции y = f(x).