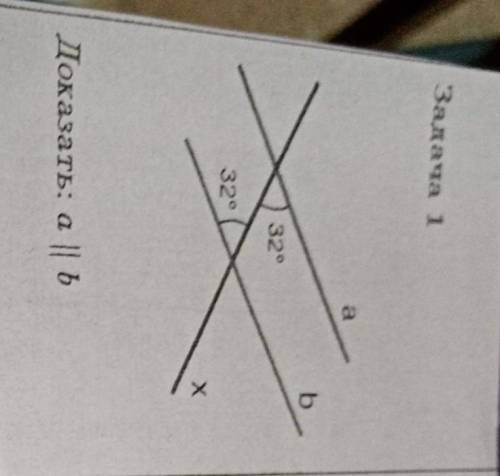
Задача 1
a
Б
32°
32°
Х
Доказать: a || b​

Данная задача требует нам показать, что прямая a параллельна прямой b.

Для начала, давайте разберемся, что значит, что две прямые параллельны. Две прямые считаются параллельными, когда они не пересекаются и находятся в одной плоскости. Значит, если мы сможем доказать, что две прямые не пересекаются и находятся в одной плоскости, то мы сможем сделать вывод, что они параллельны.

Давайте рассмотрим данный треугольник ABC. У нас есть две стороны треугольника АС и ВС, которые равны по условию задачи. Значит, треугольник АСВ является равнобедренным (так как AC = BC).

Затем, у нас есть два угла треугольника ACС и BСС, которые также равны по условию задачи (они обозначены как 32°). Значит, треугольник ACС также равносторонний (так как у него два равных угла).

Так как треугольник ACС равносторонний, то у него все стороны равны, включая сторону AC и сторону AB.

Далее, обратите внимание на отмеченную точку Х на рисунке. Линия, идущая из точки Х и пересекающая стороны треугольника AC и AB, образует углы треугольника. Назовем эти углы m и n.

Так как треугольник ACС равнобедренный, то углы ACС и СAC являются равными и равными 32° по условию задачи. Это значит, что угол n, образованный в этом равнобедренном треугольнике, также равен 32°.

Теперь рассмотрим треугольник ABC в целом. У нас есть угол n, который равен 32°, и угол B внешний по отношению к этому треугольнику. Внешний угол треугольника равен сумме двух внутренних углов этого треугольника.

Таким образом, угол B равен m + n.

Но угол m и угол n по условию задачи равны 32°. Значит, угол B равен 32° + 32° = 64°.

Итак, у нас есть два равных угла в треугольнике ABC: угол B равен 64°, а угол А у нас задан как прямой угол (равный 90°).

Третий угол треугольника ABC можно найти, используя свойство, что сумма всех углов треугольника равна 180°.

180° = 90° + 64° + угол C.

Перенесем все известные значения на одну сторону уравнения:

180° - 90° - 64° = угол C.

И, наконец, вычисляем:

26° = угол C.

Теперь давайте сделаем вывод. Мы рассмотрели треугольник ABC и доказали, что его три угла равны 90°, 64° и 26°. Это значит, что треугольник ABC является прямоугольным треугольником.

Теперь мы можем сделать заключение. Прямая a проходит через одну из вершин прямоугольного треугольника (точку А), а прямая b проходит через другую вершину треугольника (точку В).

Так как прямая a и прямая b пересекаются в вершине треугольника, а треугольник ABC является прямоугольным, то прямая a образует прямой угол с третьей стороной треугольника (стороной BC), а значит, a параллельна BC.

Поскольку сторона BC принадлежит треугольнику ABC, то прямая a параллельна самому треугольнику, и в частности, прямой ВС. Таким образом, прямая a также параллельна исходной прямой b.

Итак, мы доказали, что прямая a параллельна прямой b.