Задача 1. Миша принимает участие в онлайн-марафоне по решению задач по математике. Ежедневно он удваивает количество решенных задач по сравнению с предыдущим днем. 16 октября Миша решил за день ровно 768 задач. Какое утверждение является верным? 1) 8 октября этого же года Миша решил за день ровно 384 задачи.
2) 15 октября этого же года Миша решил за день ровно 384 задачи.
3) Невозможно определить тот день, когда Миша решил за день ровно 384 задачи.

Задание 2. Велосипедист может проехать расстояние между Гусевым и Черняховском за 2 часа, а пешеход преодолеет это расстояние за 5 часов 30 минут. Через какое время они встретятся, если отправятся одновременно из этих городов навстречу друг другу?
1) 1 час 12 минут
2) 1 час 28 минут
3) 1 час 30 минут

Задание 3. В треугольнике ABC известны длины сторон: AB = 13, BC = 14 и AC = 15. Выберите верное утверждение.
1) Одна из высот треугольника равна 12.
2) Одна из высот треугольника равна 16.
3) Ни одна высота этого треугольника не имеет целочисленной длины.

Задание 4. Парабола, заданная уравнением x = ay2 + by + c, проходит через точки (1, 0), (1, −2) и (4, 1). Найдите x, если y = 2.

Задание 5. Сумма двух натуральных чисел равна 2021, а их наименьшее общее кратное равно 21620. Найдите наибольший общий делитель этих двух чисел.

Задание 6. При каких значениях параметра a уравнение −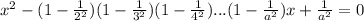 имеет хотя бы одно решение? В ответ запишите сумму наибольшего отрицательного и наименьшего положительного из найденных значений a.

Задание 7. В параллелограмме ABCD на диагонали AC взята точка E такая, что AE : EC = 1 : 3. В треугольнике ACD проведена медиана DF и на этой медиане взята точка G такая, что DG : GF = 2 : 1. Найдите площадь параллелограмма ABCD, если известно, что площадь четырехугольника AEGD равна 36.

Задание 8. В треугольнике ABC проведена биссектриса AD. На стороне AC треугольника отмечена точка E такая, что треугольники ABC и EDC подобны, но стороны AB и ED не параллельны. Найдите ED, если BD = 4, а DC = 5.

Даша5432111    2   10.09.2020 22:46    236