за простейшие уравнения 2³√x+1-⁶√x+1=6 (7x+2)√4x-3x²-1=0
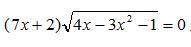
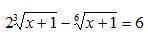
Другие вопросы по теме Математика
Популярные вопросы
- Составьте 5 предложений со словами/фразами: citizen community respect obey laws...
1 - в трапеции abcd на боковых сторонах ab и cd отмечены точки k и e соответственно.Найдите...
1 - Төмендегі фигураның ауданы мен периметріе тап 3x+2y 2x+y ...
1 - Жаркент өңірі туралы шағын мақала? Немесе Оқушы бойында адамзаттық құндылықтарды...
2 - Не выполняя арифметические действия,покажите что: сумма 56+96 делиться на 8 СОЧ...
3 - На рисунке четырехугольник ABCD- ромб, угол А которого равен 60°.Найдите угол...
3 - . А.Выпишите схему, правильно отражающую систематическое положение белого медведя....
3 - Можно ответ СОЧ Найдите пириметр фигуры:2 А3В+3А24 А3В3А3В-5А2+4ВЗаранее...
1 - На рисунке закрашены регионы распространения одной из основных рас мира....
1 - РУССКИЙ ЯЗЫКВ 13-ом предложении определите разряд прилагательных * Таинственный...
2
У нас есть два уравнения вида:
2³√(x+1) - ⁶√(x+1) = 6 и (7x+2)√(4x-3x²-1) = 0.
Для начала, давайте решим первое уравнение:
2³√(x+1) - ⁶√(x+1) = 6
Для удобства рассмотрим замену переменной:
y = √(x+1)
Тогда уравнение примет следующий вид:
2³y - ⁶y = 6
Теперь у нас есть простое уравнение, которое мы можем решить:
8y - 64y = 6
-56y = 6
Теперь давайте найдем значение y:
y = -6/56
y = -3/28
Теперь, чтобы найти x, мы должны вернуться к начальному уравнению и подставить найденное значение y:
√(x+1) = -3/28
x + 1 = (-3/28)²
x + 1 = 9/784
x = 9/784 - 1
x = 9/784 - 784/784
x = -775/784
Теперь перейдем ко второму уравнению:
(7x+2)√(4x-3x²-1) = 0
У нас есть два множителя: (7x+2) и √(4x-3x²-1). Так как произведение равно нулю, один из множителей должен быть равен нулю:
7x + 2 = 0 или √(4x-3x²-1) = 0
Решим сначала первое уравнение:
7x + 2 = 0
7x = -2
x = -2/7
Теперь решим второе уравнение:
√(4x-3x²-1) = 0
Сначала заметим, что радикаль может быть равен нулю при условии, что выражение под радикалом равно нулю:
4x - 3x² - 1 = 0
Решим это уравнение.
Сначала перенесем все коэффициенты в левую часть:
3x² - 4x + 1 = 0
Теперь используем метод факторизации или квадратное уравнение:
(3x - 1)(x - 1) = 0
Теперь, используя свойство нулевого произведения, мы получаем два возможных значения для x:
3x - 1 = 0 или x - 1 = 0
3x = 1 или x = 1
x = 1/3 или x = 1
Таким образом, уравнение имеет три решения: x = -775/784, x = -2/7, и x = 1/3.
Это ответ на исходное уравнение.