Y"+y'-20=6x-2-x^2
y(1) =2
y'(1) =5
решите дифференциальное уравнение первого вида, , ! теорема виета.

Ответы

anonim869 11.10.2020 00:09

y"+y'=6x+18-x^2

Характеристическое уравнение однородного: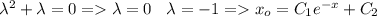 $\lambda^2+\lambda=0=\lambda=0\:\:\:\:\lambda=-1=x_o=C_1e^{-x}+C_2$

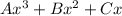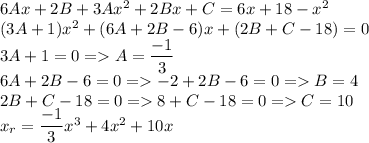
Частное решение ищем в виде Ax^3+Bx^2+Cx : $6Ax+2B+3Ax^2+2Bx+C=6x+18-x^2\\ (3A+1)x^2+(6A+2B-6)x+(2B+C-18)=0\\ 3A+1=0=A=\dfrac{-1}{3}\\ 6A+2B-6=0=-2+2B-6=0=B=4\\ 2B+C-18=0=8+C-18=0=C=10\\ x_r=\dfrac{-1}{3}x^3+4x^2+10x$

Тогда общее решение $x=x_o+x_r=C_1e^{-x}+C_2-\dfrac{1}{3}x^3+4x^2+10x$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

ayaulym10 12.09.2019 14:00

Объясните как происходит это преобразование sin5x+sin3x-sin4x=0 2sin4x*cosx-sin4x=0...

axon11kot 12.09.2019 14:00

Объясните, что за процесс представлен схемой. заряженные частицы - электрические взаимодействия - возникновение ионизации - изменения - биологические эффекты нужно...

тупойчеловек376 12.09.2019 14:00

Придумать волшебную сказку о поведении в школе где-то 15длинных предложений или кратких предложений 25 . !...

максим1723 12.09.2019 14:00

Из поселка одновременно в протиположныз направлениях вышел пешеход и выехал велосипедист. когда велрсипедист проехал 22 км/ ч со скоростью 11 км/ ч, расстояние между ними...

Зефирка78 12.09.2019 14:00

Во дворе бегают куры и поросята у всех 20 голов и 52 ноги сколько кур и поросят зарание...

StefaLandon 12.09.2019 14:00

Решите уравнение 84: х=6 умножить на 7...

ZA25 12.09.2019 14:00

Верны ли высказывания? число 80 не больше числа 65,число 70 не меньше числа 65? составь истинные высказывания без слова не...

3lJouKpolJouk 12.09.2019 14:00

Вмагазин 8 корзин клубники по 7 кг в каждой,5 корзин продали,сколько килограммов клубники осталось продать?...

kurban052 12.09.2019 14:00

Выражение 163+37х+18х х=3 х=10 и реши его...

Angela8689 12.09.2019 14:00

Выбери последовательность операции,в результате выполнения которых получится исходное число. а) увеличить на 13, уменьшить на 23, вычесть 13, прибавить 20 b) увеличить...

Y"+y'-20=6x-2-x^2 y(1) =2 y'(1) =5 решите дифференциальное уравнение первого вида, , ! теорема виета.

Популярные вопросы

Y"+y'-20=6x-2-x^2
y(1) =2
y'(1) =5
решите дифференциальное уравнение первого вида, , ! теорема виета.