1. Математика
  2. Y=tg^3×2x:lg(5x+1)Найдите

Y=tg^3×2x:lg(5x+1)

Найдите производную

Apelsinka032 Apelsinka032    2   31.10.2020 23:53    0

Ответы
Sachak95 Sachak95  30.11.2020 23:54

\dfrac{\Big(\dfrac{18x\b{tg}^2x}{\cos^23x}+2\b{tg}^3x\Big)\lg(5x+1)-\dfrac{10\b {tg}^3x\cdotx}{x\ln10}}{\lg^2(5x+1)}

Пошаговое объяснение:

1 Запишем

\Bigg(\dfrac{\b {tg}^3x\cdot2x}{\lg(5x+1)}\Bigg)'

2 Производная частного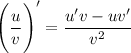 \Bigg(\dfrac uv\Bigg)'=\dfrac{u'v-uv'}{v^2}

\dfrac{\big(\b {tg}^3x\cdot2x\big)'\lg(5x+1)-\b {tg}^3x\cdot2x\lg'(5x+1)}{\lg^2(5x+1)}

3 Производная произведения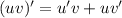 (uv)'=u'v+uv'

\dfrac{(2x\b{tg}^3x'+2\b{tg}^3x)\lg(5x+1)-\b {tg}^3x\cdot2x\lg'(5x+1)}{\lg^2(5x+1)}

4 Производная тангенса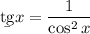 \b{tg}x=\dfrac1{\cos^2x} и производная сложной функции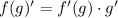 f(g)'=f'(g)\cdot g'

\dfrac{(18x\b{tg}^2x\dfrac1{\cos^23x}+2\b{tg}^3x)\lg(5x+1)-\b {tg}^3x\cdot2x\lg'(5x+1)}{\lg^2(5x+1)}

5 Производная логарифма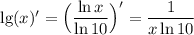 \lg(x)'=\Big(\dfrac{\ln x}{\ln 10}\Big)'=\dfrac1{x\ln10}

\dfrac{(18x\b{tg}^2x\dfrac1{\cos^23x}+2\b{tg}^3x)\lg(5x+1)-\b {tg}^3x\cdot2x\dfrac5{x\ln10}}{\lg^2(5x+1)}

6 Подгоним все под одну дробь

\dfrac{\Big(\dfrac{18x\b{tg}^2x}{\cos^23x}+2\b{tg}^3x\Big)\lg(5x+1)-\dfrac{10\b {tg}^3x\cdotx}{x\ln10}}{\lg^2(5x+1)}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Amelia2018 Amelia2018  26.05.2019 22:30
За 7 год у басейн налилося 224 л води.за який час у нього наллєтьсч 228 л води.? буду вам вдячна! )...
vakfor vakfor  26.05.2019 22:30
Після того як учень прочитав 8/11 книжки , виявилось що частина яку залишилось прочитати , на 75 сторінок менша від прочитаної. скільки сторінок у книжці...
vitalia4420 vitalia4420  26.05.2019 22:30
Завтобуса вийшли 32 пасажири, залишилося у 8 раз менше, ніж вийшло. скільки пасажирів було в автобусі спочатку?...
20071218hi 20071218hi  26.05.2019 22:30
Выразите в граммах и килограммах - 1) 9675г 2)14300г 3)21060г 4)7004г...
OniksX OniksX  26.05.2019 22:30
Примените распределительное свойство умножения: 11*(60+а),21*(38--9)*24,(y+4)*38. *-это умножение....
100132 100132  26.05.2019 22:30
Цена некорого товара 98 р. за 1 кг. сколько купили этого товара, если за покупку заплатили 34,3 р? 441 р ?...
nikolajsagirov nikolajsagirov  26.05.2019 22:30
5/8 * на одну целую 13/15 и * на две целых 2/7...
maxcarleson1 maxcarleson1  26.05.2019 22:30
Дополни таким числом чтобы ее можно было решить тремя реши составляя выражения.в одной коробке было 6 карандашей а в другой 12 каранд.катя взяла? ? каранд.сколько...
lenaprivet lenaprivet  26.05.2019 22:30
Как решить демидова (2 часть) 4 класс как решить демидова 4 класс страница 3 внизу, последний абзац. можно ответы? если сойдутся с моими, то самого решения просить...
Васелёк05 Васелёк05  26.05.2019 22:30
Найдите значение частного a: b 1)a=5*7*13,b=7*13 2)a=11*13*41,b=11*41 3)a=7*3*19,b=7*19 4)a=2*2*41,b=2*41 5)a=3*3*29,b=3*29 6)a=2*11*37,b=2*37...

Популярные вопросы