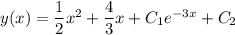y’’+3y’=3x+5 найти общее решение линейного неоднородного уравнение второго порядка с постоянными коэффициэнтами
Другие вопросы по теме Математика
Популярные вопросы
- моя жизнь в ваших руках так как у меня сор а я не выполнела Установите соответствие...
3 - Творча спадщина Богдана Хмельницкого...
3 - ОТ НЕ БЕРИЬЕ ИЗ ИНТЕРНЕТА ТАМ ПОДРУГОМУ ВОПРОС ЗАДАН Если коснуться шарика электроскопа...
2 - Металеві форми для виливання супозиторіїв попередньо замазують ?...
2 - ЗА РЕШЕНИЕ ЗАДАЧИошибся с , см другой пост...
3 - Написати листа Скруджу ( Різдвяна пісня у прозі)...
1 - Западную группу кыргызов выходи...
3 - Придумай свою историю о честности и искренности и напиши...
1 - Для каждого значения а определить количество решений уравнения...
3 - қайыршы антонға бейтаныс кісінің ақылы қалай әсер еткенін тұжырымдап, өз пікіріңізді...
3
1) Решим сопряжённое однородное ДУ:
2) Найдём частное решение ДУ:
Потому как одно из характеристических чисел (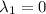 ) совпадает со степенью при экспоненте в квазимногочлене неоднородности (
) совпадает со степенью при экспоненте в квазимногочлене неоднородности (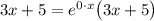 ) с кратностью 1, то ищем частное решение в виде многочлена на одну степень больше (причём оно определится неоднозначно):
) с кратностью 1, то ищем частное решение в виде многочлена на одну степень больше (причём оно определится неоднозначно):
3) Обозначая сумму двух произвольных констант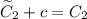 , получим
, получим
ответ.