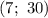Y=3x-ln(x-6)^3+9
Точка минимума
Другие вопросы по теме Математика
Популярные вопросы
- 3333=33 для 2 класс как получить 33...
2 - 7- topshiriq. Matnni o qing va topshiriqlarni bajaring...
3 - Які повноваження в депутатів? Як його выберают? ...
2 - Укажите основные характеристики современного объектно-ориентированного графического...
2 - Краткое сообщение о людях труда по ОДНК...
1 - Ежелгы Кытайдын мемлекеттеры (4 мемлекет) Билеушылеры (4 мемлекеттын билеушылеры)...
3 - У рівнобедренний прямокутний трикутник АВС вписано прямокутник,який має з...
3 - Установите соответствие между растениями (1-4) и их вегетативного размножения...
3 - Қаннан өз пигменттері, ауыр металдардың тұздары шығатын мүше...
3 - Графиком какой функции является гипербола y=7x² , y=6x , y=6x-⅐ , ни одной...
2
ОДЗ: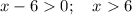
Найдем производную для заданной функции:
Найдем стационарные (критические) точки. Для этого приравняем производную к нулю:
Следовательно, абсцисса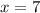 — возможно, абсцисса точки экстремума — точка, при переходе через которую производная меняет знак. Если производная меняет знак с "–" на "+", то это точка минимума, если производная меняет знак с "+" на "–", то это точка максимума.
— возможно, абсцисса точки экстремума — точка, при переходе через которую производная меняет знак. Если производная меняет знак с "–" на "+", то это точка минимума, если производная меняет знак с "+" на "–", то это точка максимума.
Рассмотрим промежуток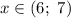 :
:
Возьмем, например, абсциссу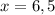 и подставим ее в производную:
и подставим ее в производную:
Рассмотрим промежуток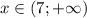 :
:
Возьмем, например, абсциссу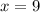 и подставим ее в производную:
и подставим ее в производную:
Следовательно,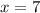 — абсцисса точки экстремума, а именно абсцисса точки минимума, так как производная меняет знак с "–" на "+". Тогда значение ординаты
— абсцисса точки экстремума, а именно абсцисса точки минимума, так как производная меняет знак с "–" на "+". Тогда значение ординаты 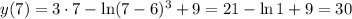
ответ: точка