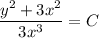Xy^2y'=x^2+y^3 дифферинциальное уравнение.
Другие вопросы по теме Математика
Популярные вопросы
- Поделите на 3 колонки, растительноядные, плодоядные,всеядные Потом...
1 - С ТЕСПОМ ПО И С Тургенев Бежин луг...
3 - Діаграма стану заліза вуглець(Fe1)...
1 - Эххх опять будет 3 по матике...
3 - Do or Does Образец DOES Mark have an art lesson on Monday ? - Yes...
1 - Если у кого-то есть такая тетрадь скиньте ответы в конце! у меня...
2 - 3-тапсырма.Наполеон соғыстарының әлемдік саясаттың өзгеруіне ықпалын...
3 - Доведіть, що число 3⁷+3⁹-9⁴ кратне числу...
1 - 2. Автор а ң жас кезі мен ұлғайған шағындағы бойда болатын өзгерістерін...
1 - 342.По какому принципу продолжает финансироваться наука и образование...
2
Умножим дифференциальное уравнение на интегрирующий множитель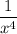 . Тогда уравнение примет вид
. Тогда уравнение примет вид
Заметим, что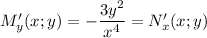 , т.е. дифференциальное уравнение является уравнением в полных дифференциалах.
, т.е. дифференциальное уравнение является уравнением в полных дифференциалах.
Интегрируем функцию F сначала по х: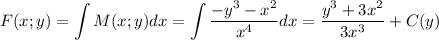
Теперь продифференцируем по переменной у:
Общий интеграл: