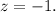X+y+z=0
2x+3y+z=0
(x+1)^2+(y+2)^2+(z+3)^2 = 14
Другие вопросы по теме Математика
Популярные вопросы
- Изобразите схему образования оксида бария ВаО с диаграммы «точек...
2 - Сенын ойынша окига неден басталды...
2 - Ионная АтомнаяМолекулярнаяМеталлическаякакая из схем отражает строение...
2 - Алгебра ТЖБ помагите 7класс 3четвергь...
3 - Задание. Напишите выражкние на языке программы Phyton Информатика...
3 - ДАЮ ЭТО СОЧ ТЕКСТ ЗАДАНИЯ 6. Жазылым Берілген тақырыптардың бірін...
2 - 1. Найдите и укажите строку, в которой правильно характеризуется...
1 - Су Сусыз өмір сүру мүмкін емес. Жер бетінің төрттен үш бөлігін су...
3 - Библиотека состоит из 15 различных книг, причем 5 книг стоят по 4...
1 - , решить эти не понятные для меня задания, надо...
1
Пошаговое объяснение:
Вычтем из второго уравнения системы первое:
откуда
Подставляя это выражение в первое уравнение, получим
Подставляем найденные значения в третье уравнение и пользуемся формулой квадрата суммы :
:
Подставляя полученные значения в выражения для и
и  получаем при
получаем при 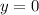
 и
и  при
при 
 и
и