1. Математика
  2. X²+px+24=0,если известно

X²+px+24=0,если известно что его корни положительны и их разность равна 2

serbakovasvetas serbakovasvetas    2   04.08.2020 12:40    3

Ответы
Marka9696 Marka9696  15.10.2020 15:42

-10

Пошаговое объяснение:

По теореме Виета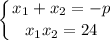 \displaystyle \left \{ {{x_1+x_2=-p} \atop {x_1x_2=24}} \right.

x_1-x_2=2\\(x_1-x_2)^2=4\\x_1^2-2x_1x_2+x_2^2=4\\x_1^2+2x_1x_2+x_2^2-4x_1x_2=4\\(x_1+x_2)^2-4x_1x_2=4\\p^2-4\cdot 24=4\\p^2=100\\p=\pm 10

Так как корни положительны, их сумма также положительна, поэтому -p > 0, p < 0, p = -10. Действительно, уравнение x²-10x+24 = 0 имеет корни 4 и 6, что подходит условию.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
artchapyshev artchapyshev  02.07.2019 07:50
Разложите на множители: a^3 -3b+a^2b -3a...
ммрк ммрк  02.07.2019 07:50
Как можно назвать одним словом треугольник прямоугольник и квадрат...
Евдокия47 Евдокия47  02.07.2019 07:50
Продолжи ряды чисел.3 1 1 5 5 5 3 1 1 6 6 6 3 1 1 7 7 7...
1luvash 1luvash  02.07.2019 07:50
Возраст иры ,её старшейсестры,мамы,бабушки всё это делителичисла 165.найдите возраст всех , если известно ире 11. лет....
elenanatalja elenanatalja  02.07.2019 07:50
Переведите в римские числа 18064802009...
BusL81 BusL81  02.07.2019 08:00
Как решить уравнение 4×(3-x)-11=7×(2x-5)...
юська3 юська3  02.07.2019 08:00
Как решить в одной корзине 112 яблок , что вдвое больше , чем в другой,сколько яблок в двух корзинах?...
хочузнать2018 хочузнать2018  02.07.2019 08:00
Составте 5 предложений на существительное...
Кет1235 Кет1235  02.07.2019 08:00
По действиям (96,6+98,6): 6,4*1,2-0,2=...
vovashkaruba vovashkaruba  02.07.2019 08:00
Найдите значение выражения (7,6 – 2,16) ∙ 3,5 : 0,04....

Популярные вопросы