X*((arcctg^2)x)*dx
решить интегралл
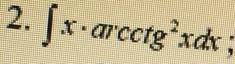
Другие вопросы по теме Математика
Популярные вопросы
- S= 1 км, m=50 кг, N=0,2, Найдите A...
2 - Установіть співвіднесеність між героєм та його вчинками...
3 - Напишите небольшое сочинение по картине не брать из интернета!...
2 - У багажник автомобіля поклали 5 мішків цукру і 4 мішки борошна.Виявилось,що загальний...
1 - на данному колі побудуйте точку яка знаходиться на даній відстані від даної прямої.Скількі...
1 - До 500 г розчину натрій хлориду з масовою часикою розчиненої речовини 10% додали...
2 - Яка маса сульфур (IV) оксиду прореагувала з водою, якщо в результаті утворилося...
1 - докажите используя текст стихотворения что его герой не ищет гармонии в природе...
3 - Провідність електролітів при охолодженні -...
3 - Кому нужны балы?крч просто напишите в ответе и всё...
3
ответ: Применяем метод интегрирования по частям и введение под знак дифференциала
Пошаговое объяснение: 1) ∫x·arсtg²xdx= (пусть arсtg²x=U, xdx=dV; тогда 2arctgx dx ·(1/1+x²) = dU, x²/2=dV) =(x²/2)·arсtg²x - (1/2)∫x²2arctgx·dx/(1+x²)= (x²/2)·arсtg²x - ∫x²arctgx dx/ (1+x²) ;
2) Вычислим ∫x²arctgx dx/ (1+x²) =∫(аrctg x - arctg x/(1+x²))dx =∫аrctg x dx - ∫arctg x/(1+x²))dx;
3)∫аrctg x dx=(U=arctg x, dV=dx ⇒dU=1/(1+x²)dx, V=x) =x·arctg x - ∫xdx(1+x²) =x·arctg x - (1/2)·∫d(x²)/(1+x²) =x·arctg x - (1/2)·ln(x²+1) 4) ∫arctg x/(1+x²))dx = ∫d(arctg x)/(1+x²) = (1/2)·arctg²x
Итак: ∫x·arсtg²xdx= (x²/2)·arсtg²x - ∫x²arctgx dx/ (1+x²)=(x²/2)·arсtg²x + (1/2)·ln (x²+1) - x·arctg x + (1/2)·arctg²x +C