(x^2+x)^2 + (x^2 + x)-2 = 0.
Другие вопросы по теме Математика
Популярные вопросы
- Математика первые 2 задания можно пропустить главное остальное!...
2 - Почему мхи живут во влажных местах? Тут требуемся как можно более подробный...
3 - Дано: ∢1=158°,∢5=31°. Вычисли остальные углы. u3.PNG ∢1= °;∢2= °;∢3= °;∢4=...
3 - В калориметр масою 200г у якому міститься холодна вода доливають гарячу воду...
2 - Написать эссе-рассуждение на тему «Мировое значение романа «Война и мир»....
1 - Какой вклад внесли древние египтяне в развитие Астрономии, математики, медицины?...
1 - дано: треугольник АВС, АВ 4 см,ВС 9 см,ВН высота треугольника АВС, ВН 3 см,...
3 - «Что я чувствую, слушая музыку А. Моцарта».—эссе ...
1 - Кусок льда массой 2 кг, взятой при температуре -5 градусов по цельсию, кладут...
1 - Нужен ПОЛНЫЙ анализ данного стиха Пастернака: Страшная сказка Всё переменится...
2
Замена:
Обратная замена:
Нет корней
ответ: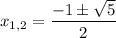
Пошаговое объяснение:
(x²+x)²+ (x² + x)-2 = 0.
x² + x=t
t²+t-2=0