||x^2-3x|-5|=x+1 решить уравнение
Другие вопросы по теме Математика
Популярные вопросы
- 50 вопрос: молодые авиамоделисты николай и алексей экспериментировали со...
3 - Определить вид , переходность , возвратность , спряжение , глагола - побродить....
3 - Use the correct form of the present simple or the present perfect simple...
3 - Разобраться с этим вопросом ! 6и 7...
3 - Отзыв на тему: что общего между тремя произведения, далёкие зимние вечера,...
3 - Изложениепо фильму мост в терабитию на ...
1 - Административное устройство колоний (испанская колонизация латинской америки)...
3 - Нужен доклад по обществознанию на тему: человек, образование, общество (одна...
2 - Написать сообщение,возникновение земли и её геологическая эры,периуды...
2 - Напишите сказку о инерции. небольшую и не маленькую...
1
ответ: x1=2± x2=1±i
x2=1±i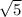 x3=1±
x3=1±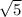 x4=2
x4=2
Пошаговое объяснение:
пусть x^2-3x=y (Чтобы много не писать)
||y|-5|=x+1
|y|-5=x+1 |y|-5=-x-1
|y|=x+6 |y|=4-x
y=x+6 y=-x-6 y=4-x y=x-4
x^2-3x=x+6 x^2-3x=-x-6 x^2-3x=4-x x^2-3x=x-4
x^2-4x-6=0 x^2-2x+6=0 x^2-2x-4=0 x^2-4x+4=0
D=40 D=-20 D=20 D=0
x1=2± x2=1±i
x2=1±i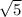 x3=1±
x3=1±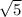 x4=2
x4=2