X²=18+y² решите уравнение с целыми числами. Попалась задача на одимпиаде, написал нет решений может вы найдете, просто значально в задаче намекают на подбор. Полный квадрат извлекал, ничего не вышло

Ответы

Gonsh1240 04.12.2020 16:12

ответ:В целых числах нет решенийПошаговое объяснение:Подбором тут можно:

Преобразуем равенство

$x^2=18+y^2\\x^2-y^2=18\\(x-y)(x+y)=18$

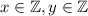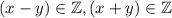Так как $x\in\mathbb Z, y\in\mathbb Z$ то и $(x-y)\in\mathbb Z,(x+y)\in\mathbb Z$ тогда мы можем представить это в виде произведения целых чисел, тогда имеем варианты

$\displaystyle \left[\begin{array}{ccc}\left\{\begin{array}{ccc}x-y=18\\x+y=1\end{array}\right.\\\left\{\begin{array}{ccc}x-y=1\\x+y=18\end{array}\right.\\\left\{\begin{array}{ccc}x-y=9\\x+y=2\end{array}\right.\\\left\{\begin{array}{ccc}x-y=2\\x+y=9\end{array}\right. \\\left\{\begin{array}{ccc}x-y=6\\x+y=3\end{array}\right.\\\left\{\begin{array}{ccc}x-y=3\\x+y=6\end{array}\right.\end{array}\right.$

$\displaystyle \left[\begin{array}{ccc}\left\{\begin{array}{ccc}x-y=-18\\x+y=-1\end{array}\right.\\\left\{\begin{array}{ccc}x-y=-1\\x+y=-18\end{array}\right.\\\left\{\begin{array}{ccc}x-y=-9\\x+y=-2\end{array}\right.\\\left\{\begin{array}{ccc}x-y=-2\\x+y=-9\end{array}\right. \\\left\{\begin{array}{ccc}x-y=-6\\x+y=-3\end{array}\right.\\\left\{\begin{array}{ccc}x-y=-3\\x+y=-6\end{array}\right.\end{array}\right.$

Ну и просто методом сложения получаем что решений в целых числах нет, ведь при сложении строк системы получаем равенство 2х = нечетное число, что не имеет решений в целых числах.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика