Выясните чётной или нечётной является функция:
б,в,г
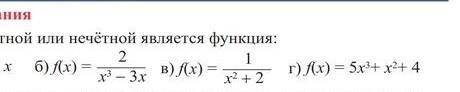
Другие вопросы по теме Математика
Популярные вопросы
- Приведите пример произведения, в котором автор пытается передать...
3 - РЕШИТЕ Даны две стороны треугольника и угол между ними.Найдите третью...
2 - Найти нужно AB. Подскажите НУЖНО!!...
2 - Какие факторы повлияли на развитие науки и техники в 18 веке в России...
3 - Привет всем нужно писать расказ,6-7 предложение на тему о Правилах...
2 - Хайуанаттар бағындағы жануарлар үшін бір бригада 7/10 т екіншісі...
2 - Составьте и творческих во по рассказу перепёлка...
3 - Сюжет Русалонька из 7-в або прокляття роду Кулакивський...
3 - Великий поршень гідравлічного преса стискає деталь із силою з мн....
2 - Минимальное расстояние Луны от Земли 365200км., а максимальное 403600км....
1
Если для любого из области определения функции выполняется равенство
из области определения функции выполняется равенство 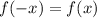 , то функция является чётной.
, то функция является чётной.
Если для любого из области определения функции выполняется равенство
из области определения функции выполняется равенство 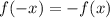 , то данная функция является нечётной.
, то данная функция является нечётной.
Если же ни одно из этих равенств не выполняется, то функция не является ни чётной, ни нечётной.
б)
Отсюда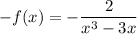 .
.
Для начала найдём область определения данной функции. Её знаменатель не должен быть равен нулю:
Итак, область определения нашли. Теперь найдём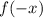 , для этого все
, для этого все  в функции заменим на
в функции заменим на 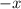 .
.
Таким образом, данная функция является нечётной.
в)
Отсюда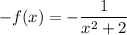 .
.
Для начала найдём область определения данной функции. Её знаменатель не должен быть равен нулю:
То есть, для данной функции за можно принять любое действительное число. Теперь найдём
можно принять любое действительное число. Теперь найдём 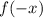 , для этого все
, для этого все  в функции заменим на
в функции заменим на 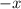 .
.
Таким образом, данная функция является чётной.
г)
Отсюда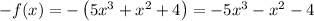 .
.